题目内容
已知f(x)是定义在R上的函数,f(-x)=f(x)且f(x)=f(x+2),当0≤x≤1时,f(x)=x2,若方程f(x)=x+a有两个不等实根,那么实数a的值为( )
A、2k或2k-
| ||
B、k或k-
| ||
| C、2k(k∈z) | ||
| D、k(k∈z) |
考点:函数的周期性,函数奇偶性的性质,一元二次方程的根的分布与系数的关系
专题:数形结合,转化思想
分析:由已知中f(x)是定义在R上的函数,f(-x)=f(x)且f(x)=f(x+2),当0≤x≤1时,f(x)=x2,画出f(x)的图象,数形结合可得满足条件的实数a的值.
解答:
解:∵f(x)是定义在R上的函数,f(-x)=f(x)且f(x)=f(x+2),
故f(x)为偶函数,且是以2为周期的周期函数,
又∵当0≤x≤1时,f(x)=x2,
∴f(x)的图象如下图所示:
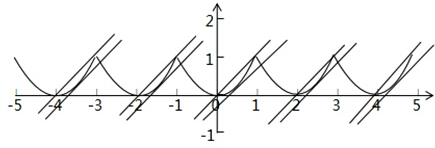
由图可得:在[0,1]上,当a=0或a=-
时,方程f(x)=x+a有两个不等实根,
故实数a的值为2k或2k-
(k∈z),
故选:A
故f(x)为偶函数,且是以2为周期的周期函数,
又∵当0≤x≤1时,f(x)=x2,
∴f(x)的图象如下图所示:

由图可得:在[0,1]上,当a=0或a=-
| 1 |
| 4 |
故实数a的值为2k或2k-
| 1 |
| 4 |
故选:A
点评:本题考查的知识点是函数的图象和性质,函数的零点,是函数问题的综合应用,难度中档.

练习册系列答案
相关题目
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A、若α⊥β,m?α,则m⊥β |
| B、若α∥β,m?α,n?β,则m∥n |
| C、若m∥α,n?α则m∥n |
| D、若m⊥α,m∥β,则α⊥β |
某校150名教职工中,有老年人20个,中年人50个,青年人80个,从中抽取30个作为样本.
①采用随机抽样法:抽签取出30个样本;
②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本;
③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本.
下列说法中正确的是( )
①采用随机抽样法:抽签取出30个样本;
②采用系统抽样法:将教工编号为00,01,…,149,然后平均分组抽取30个样本;
③采用分层抽样法:从老年人,中年人,青年人中抽取30个样本.
下列说法中正确的是( )
| A、无论采用哪种方法,这150个教工中每一个被抽到的概率都相等 |
| B、①②两种抽样方法,这150个教工中每一个被抽到的概率都相等;③并非如此 |
| C、①③两种抽样方法,这150个教工中每一个被抽到的概率都相等;②并非如此 |
| D、采用不同的抽样方法,这150个教工中每一个被抽到的概率是各不相同的 |
一个各项均为正数的等比数列,其任何一项都等于它后面两项之和,则其公比是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
不等式(x-2)(x-1)<0的解集是( )
| A、{x|1<x<2} |
| B、{x|x<1或x>2} |
| C、{x|x<1} |
| D、{x|x>2} |
已知函数f(x)=x2-cosx,设a=f(-0.5),b=f(0),c=f(3),则( )
| A、a<b<c |
| B、c<a<b |
| C、c<b<a |
| D、b<a<c |
极坐标系中,过点(2,
)且与极轴垂直的直线方程为( )
| π |
| 3 |
A、ρsinθ=-
| ||
B、ρ=-
| ||
| C、ρ=-4cosθ | ||
| D、ρcosθ-1=0 |
已知集合M={x|
>0},N={x|-3x2+x+2>0},则M∩N=( )
| 2x-1 |
| x+1 |
| A、(-∞,-1)∪(1,+∞) | ||
B、(
| ||
| C、(1,+∞) | ||
D、(-∞,-1)∪(-
|
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.