题目内容
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3).
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
考点:直线的一般式方程
专题:直线与圆
分析:(1)由题意可得AB的斜率,可得AB边高线斜率,进而可得方程;(2)由(1)知直线AB的方程,可得C到直线AB的距离为d,由距离公式可得|AB|,代入三角形的面积公式可得.
解答:
解:(1)由题意可得kAB=
=
=6,
∴AB边高线斜率k=-
,
∴AB边上的高线的点斜式方程为y-3=-
(x-4),
化为一般式可得x+6y-22=0;
(2)由(1)知直线AB的方程为y-5=6(x+1),即6x-y+11=0,
∴C到直线AB的距离为d=
=
=
,
又∵|AB|=
=
,
∴三角形ABC的面积S=
|AB|d=
•
=16
| -1-5 |
| -2-(-1) |
| -6 |
| -1 |
∴AB边高线斜率k=-
| 1 |
| 6 |
∴AB边上的高线的点斜式方程为y-3=-
| 1 |
| 6 |
化为一般式可得x+6y-22=0;
(2)由(1)知直线AB的方程为y-5=6(x+1),即6x-y+11=0,
∴C到直线AB的距离为d=
| |24-3+11| | ||
|
| 32 | ||
|
| 32 |
| 37 |
| 37 |
又∵|AB|=
| (-1+2)2+(5+1)2 |
| 37 |
∴三角形ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 37 |
| 32 |
| 37 |
| 37 |
点评:本题考查直线的一般式方程,涉及点到直线的距离和三角形的面积,属基础题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.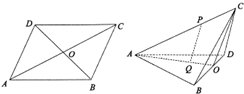 如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.
如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.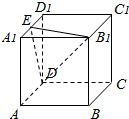 正方体ABCD-A1B1C1D1的棱长为a,点E是A1D1的中点,求点A1到平面B1DE的距离.
正方体ABCD-A1B1C1D1的棱长为a,点E是A1D1的中点,求点A1到平面B1DE的距离.