题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{log_2}x,x>0\\ ax+1,x≤0\end{array}\right.$.若a>0,则函数y=f(f(x))-1有3个零点.分析 函数y=f(f(x))-1=0,求出f(x)的值,然后利用分段函数的表达式求解x的值,推出结果.
解答 解:函数y=f(f(x))-1,令f(f(x))-1=0,
当f(x)>0时,可得log2f(x)=1,解得f(x)=2,
则log2x=2,解得x=4,ax+1=2,解得x=$\frac{1}{a}$(舍去).
当f(x)<0,可得af(x)+1=1,解得f(x)=0,
则log2x=0,解得x=1,ax+1=0,解得x=-$\frac{1}{a}$.
所以函数的零点3个.
故答案为:3.
点评 本题考查分段函数的应用,函数的零点个数的求法,考查转化思想以及计算能力.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.已知集合$A=\left\{{({x,y})|y-\sqrt{x}=0}\right\},B=\left\{{({x,y})|{x^2}+{y^2}=1}\right\}$,C=A∩B,则C的子集的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
19.下列说法正确的是( )
| A. | “?x∈R,ex>0”的否定是“?x∈R,使ex>0” | |
| B. | 若x+y≠3(x,y∈R),则x≠2或y≠1 | |
| C. | “x2+2x≥ax(1≤x≤2)恒成立”等价于“(x2+2x)min≥(ax)max(1≤x≤2)” | |
| D. | “若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
9.已知函数$f(x)=sin({ωx+φ})+1({ω>0,0≤φ≤\frac{π}{2}})$的图象的相邻两对称轴之间的距离为π,且在$x=\frac{π}{6}$时取得最大值2,若$f(α)=\frac{9}{5}$,且$\frac{π}{6}<α<\frac{2π}{3}$,则$sin({2α+\frac{2π}{3}})$的值为( )
| A. | $\frac{12}{25}$ | B. | $-\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
7.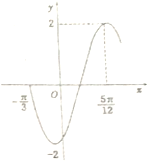 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )| A. | y=2sin(2x-$\frac{π}{6}$) | B. | y=2sin(2x+$\frac{π}{6}$) | C. | y=2sin(2x) | D. | y=2sin(2x+$\frac{π}{3}$) |
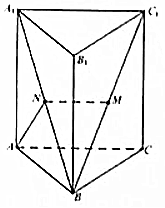 如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.
如图,直三棱柱ABC-A1B1C1中,AA1=AB,AB⊥BC,且N是A1B的中点.