题目内容
15.已知函数f(x)=2sinx+tanx-ax.(1)若曲线y=f(x)与x轴相切于原点,求a的值;
(2)若$x∈[{0\;\;,\;\;\frac{π}{2}}]$时,f(x)≥0成立,求a的取值范围.
分析 (1)求出函数的导数,计算f′(0)=0,求出a的值即可;
(2)令t=cosx,则$f'(x)=g(t)=2t+\frac{1}{t^2}-a$,t∈(0,1],通过讨论a的范围求出函数g(t)的单调性,从而进一步确定a的范围即可.
解答 解:(1)$f'(x)=2cosx+\frac{1}{{{{cos}^2}x}}-a$,由f'(0)=0,解得a=3.
(2)$x∈[{0,\frac{π}{2}})$,cosx∈(0,1].
令t=cosx,则$f'(x)=g(t)=2t+\frac{1}{t^2}-a$,t∈(0,1],$g'(t)=2-\frac{2}{t^2}≤0$,当且仅当t=1时取等号,
故t∈(0,1]时,g(t)单调递减,g(t)≥g(1)=3-a.
(ⅰ)若a≤3,则f′(x)≥0,仅当x=0时取等号,f(x)单调递增,f(x)≥f(0)=0.
(ⅱ)若a>3,令h(x)=3tanx-ax,$h'(x)=\frac{3}{{{{cos}^2}x}}-a$,存在 ${x_0}∈[{0,\frac{π}{2}})$,使得h'(x0)=0,
且当x∈(0,x0)时,h'(x)<0,h(x)单调递减,h(x)<h(0)=0,
因为 $x∈[{0,\frac{π}{2}})$,sinx≤tanx,所以f(x)≤3tanx-ax,
故存在β∈(0,x0),f(β)<0,即f(x)≥0不能恒成立,所以a>3不合题意.
综上所述,a的取值范围是(-∞,3].
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,换元思想,是一道中档题.

练习册系列答案
相关题目
3.已知集合A={x|x2-2x<0},$B=\left\{{x\left|{-\sqrt{3}<x<\sqrt{3}}\right.}\right\}$,则A∩B=( )
| A. | $\left\{{x\left|{-\sqrt{3}<x<0}\right.}\right\}$ | B. | $\left\{{x\left|{-\sqrt{3}<x<2}\right.}\right\}$ | C. | $\left\{{x\left|{0<x<\sqrt{3}}\right.}\right\}$ | D. | {x|-2<x<0} |
20.点A(2,1)到抛物线y2=ax准线的距离为1,则a的值为( )
| A. | $-\frac{1}{4}$或$-\frac{1}{12}$ | B. | $\frac{1}{4}$或$\frac{1}{12}$ | C. | -4或-12 | D. | 4或12 |
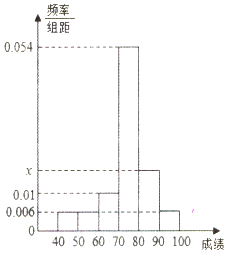 宿州市教体局为了了解2017届高三毕业生学生情况,利用分层抽样抽取50位学生数学学业水平测试成绩作调查,制作了成绩频率分布直方图,如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100).
宿州市教体局为了了解2017届高三毕业生学生情况,利用分层抽样抽取50位学生数学学业水平测试成绩作调查,制作了成绩频率分布直方图,如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100).