题目内容
6.在△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,若a2+b2-c2=$\frac{4\sqrt{3}}{3}$S.(1)求角C的大小;
(2)若c=$\sqrt{3}$,S=$\frac{\sqrt{3}}{2}$,求a+b的值.
分析 (1)利用余弦定理表示出cosC,利用面积公式表示出S,整理后代入已知等式求出tanC的值,即可确定出C的度数;
(2)由已知面积S,求出ab的值,将c,S的值代入已知等式,利用完全平方公式变形后把ab的值代入求出a+b的值即可.
解答 解:(1)∵cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,即a2+b2-c2=2abcosC,S=$\frac{1}{2}$absinC,
∴已知等式变形得:2abcosC=$\frac{4\sqrt{3}}{3}$×$\frac{1}{2}$absinC,
整理得:tanC=$\sqrt{3}$,
则C=$\frac{π}{3}$;
(2)∵c=$\sqrt{3}$,S=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{2}$,即ab=2,
∴a2+b2-3=$\frac{4\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$,即a2+b2=5,
∴(a+b)2-2ab=5,即(a+b)2=9,
则a+b=3.
点评 此题考查了余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
3.已知集合A={x|x2-2x<0},$B=\left\{{x\left|{-\sqrt{3}<x<\sqrt{3}}\right.}\right\}$,则A∩B=( )
| A. | $\left\{{x\left|{-\sqrt{3}<x<0}\right.}\right\}$ | B. | $\left\{{x\left|{-\sqrt{3}<x<2}\right.}\right\}$ | C. | $\left\{{x\left|{0<x<\sqrt{3}}\right.}\right\}$ | D. | {x|-2<x<0} |
1.设x>0,y>0,若不等式2log${\;}_{\frac{1}{2}}$[(a-1)x+ay]≤1+log${\;}_{\frac{1}{2}}$(xy)恒成立,则4a的最小值为( )
| A. | $\frac{\sqrt{6}+2}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
11.已知直线l1过直线l2:x+2y=0与l3:2x+2y-1=0的交点,与圆x2+y2+2y=0相切,则直线l1的方程是( )
| A. | 3x+4y-1=0 | B. | 3x+4y+9=0或x=1 | C. | 3x+4y+9=0 | D. | 3x+4y-1=0或x=1 |
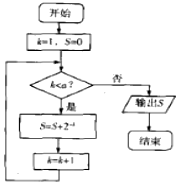
15.如图是一个程序框图,则输出的S的值是( )


| A. | 18 | B. | 20 | C. | 87 | D. | 90 |