题目内容
8.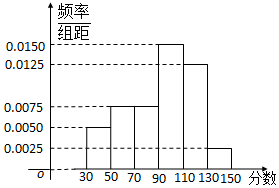 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在[30,50)和[130,150]的学生中共抽取6人,该6人中成绩在[130,150]的有几人?
(3)在(2)抽取的6人中,随机抽取3人,计分数在[130,150]内的人数为ξ,求期望E(ξ).
分析 (1)由频率分布直方图计算数据的平均分;
(2)计算样本中分数在[30,50)和[130,150]的人数,根据分层抽样原理求出抽取的人数;
(3)计算抽取的6人中分数在[130,150]的人数,求出ξ的所有取值与概率分布,计算数学期望值.
解答 解:(1)由频率分布直方图,得
该校高三学生本次数学考试的平均分为
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100
+0.0125×20×120+0.0025×20×140=92;…(4分)
(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人,
所以抽取的6人中分数在[130,150]的人有$3×\frac{6}{9}=2$(人);…(8分)
(3)由(2)知:抽取的6人中分数在[130,150]的人有2人,
依题意ξ的所有取值为0、1、2,
当ξ=0时,$P(ξ=0)=\frac{C_4^3}{C_6^3}=\frac{1}{5}$;
当ξ=1时,$P(ξ=1)=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$;
当ξ=2时,$P(ξ=2)=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$;
∴$E(ξ)=0×\frac{1}{5}+1×\frac{3}{5}+2×\frac{1}{5}=1$.…(12分)
点评 本题主要考查了频率分布直方图以及平均数和概率的计算问题,也考查了运用统计知识解决简单实际问题的能力,是基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
19.若双曲线C:x2-$\frac{y^2}{b^2}$=1(b>0)的离心率为2,则b=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
12.若x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
19.已知全集U=R,集合A={x|x<1},则∁UA=( )
| A. | (-∞,1] | B. | [1,+∞) | C. | R | D. | (1,+∞) |
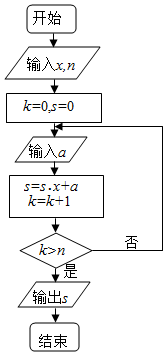 秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( )
秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值为( ) ,那么 ( )
,那么 ( ) B.
B. C.
C. D.
D.
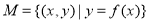 ,若对于任意
,若对于任意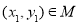 ,存在
,存在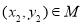 ,使得
,使得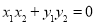 成立,则称集合
成立,则称集合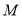 是“理想集合”.给出下列5个集合:
是“理想集合”.给出下列5个集合: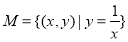 ;
;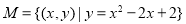 ;
; ;
;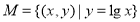 ;
; .
.