题目内容
在平面直角坐标系内,直线l的方程为ax+by+c=0,设A(x1,y1),B(x2,y2)为不同的两点,且点B不在直线l上,实数λ满足ax1+by1+c+λ(ax2+by2+c)=0.给出下列四个命题:
①不存在λ,使点A在直线l上;
②存在λ,使曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0关于直线l对称;
③若λ=-1,则过A,B两点的直线与直线l平行;
④若λ>0,则点A,B在直线l的异侧.
其中,所有真命题的序号是( )
①不存在λ,使点A在直线l上;
②存在λ,使曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0关于直线l对称;
③若λ=-1,则过A,B两点的直线与直线l平行;
④若λ>0,则点A,B在直线l的异侧.
其中,所有真命题的序号是( )
| A、①②④ | B、③④ |
| C、①②③ | D、②③④ |
考点:命题的真假判断与应用,直线的一般式方程,过两条直线交点的直线系方程
专题:直线与圆,简易逻辑
分析:①点在直线上,则点的坐标满足直线方程,从而得到ax1+by1+c=0,进而可判断①不正确.
②若λ=1,则ax1+by1+c+ax2+by2+c=0,推出直线经过的点,判断曲线是圆的方程,然后推出结果.判断②的正误;
③若λ=-1,则ax1+by1+c-(ax2+by2+c)=0,从而得到
与AB的斜率关系,即判断③的正误;
④若λ>0,利用ax2+by2+c≠0,判断ax1+by2+c与ax2+by2+c的符号,根据点与直线的位置关系从而可判定④正误.
②若λ=1,则ax1+by1+c+ax2+by2+c=0,推出直线经过的点,判断曲线是圆的方程,然后推出结果.判断②的正误;
③若λ=-1,则ax1+by1+c-(ax2+by2+c)=0,从而得到
| y2-y1 |
| x2-x1 |
④若λ>0,利用ax2+by2+c≠0,判断ax1+by2+c与ax2+by2+c的符号,根据点与直线的位置关系从而可判定④正误.
解答:
解:对于①,若点A在直线l上则ax1+by1+c=0,
∴存在实数λ=0,使点A在直线l上,
故①不正确;
对于②,若λ=1,则ax1+by1+c+ax2+by2+c=0,即a(
)+b(
)+c=0,
∴直线l经过线段AB的中点,
曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0是以AB为直径的圆的方程.
存在λ,使曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0关于直线l对称.
故②正确;
对于③,若λ=-1,则ax1+by1+c-ax2-by2-c=0
即a(x1-x2)+b(y1-y2)=0,∴
=-
直线l的方程为ax+by+c=0的斜率为:-
,
λ=-1,则过A,B两点的直线与直线l平行;
即③正确;
对于④,若λ>0,ax1+by1+c+λ(ax2+by2+c)=0,
点B不在直线l上,∴ax2+by2+c≠0,
则ax1+by1+c>0或ax2+by2+c<0,
或者ax1+by2+c<0,ax2+by2+c>0,
即点M、N在直线l的异侧,故④正确.
正确命题:②③④.
故选:D.
∴存在实数λ=0,使点A在直线l上,
故①不正确;
对于②,若λ=1,则ax1+by1+c+ax2+by2+c=0,即a(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∴直线l经过线段AB的中点,
曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0是以AB为直径的圆的方程.
存在λ,使曲线(x-x1)(x-x2)+(y-y1)(y-y2)=0关于直线l对称.
故②正确;
对于③,若λ=-1,则ax1+by1+c-ax2-by2-c=0
即a(x1-x2)+b(y1-y2)=0,∴
| y2-y1 |
| x2-x1 |
| a |
| b |
直线l的方程为ax+by+c=0的斜率为:-
| a |
| b |
λ=-1,则过A,B两点的直线与直线l平行;
即③正确;
对于④,若λ>0,ax1+by1+c+λ(ax2+by2+c)=0,
点B不在直线l上,∴ax2+by2+c≠0,
则ax1+by1+c>0或ax2+by2+c<0,
或者ax1+by2+c<0,ax2+by2+c>0,
即点M、N在直线l的异侧,故④正确.
正确命题:②③④.
故选:D.
点评:本题考查两直线的位置关系,点与直线的位置关系,直线的一般式方程等知识的综合应用,属于难题.

练习册系列答案
相关题目
已知平面直角坐标系xOy内直线l的参数方程为
(t为参数),以Ox为极轴建立极坐标系(取相同的长度单位),圆C的极坐标方程为ρ=2
sin(θ+
),则直线l与圆C的公共点的个数为 .
|
| 2 |
| π |
| 4 |
已知复数z=(a2-1)+(a-2)i(a∈R)是纯虚数,则a=( )
| A、1 | B、-1 | C、-1或1 | D、2 |
在复平面内与复数z=
所对应的点关于实轴对称的点为A,则A对应的复数为( )
| 2i |
| 1+i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |
已知点F是抛物线y2=4x焦点,M,N是该抛物线上两点,|MF|+|NF|=6,则MN中点到准线距离为( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、3+
| ||||
B、3+
| ||||
C、
| ||||
D、
|
一个几何体按比例绘制的三视图如图所示(单位:m)
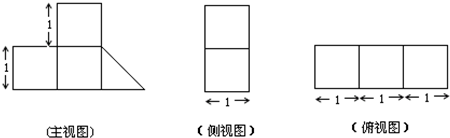
则该几何体的表面积为( )m3.

则该几何体的表面积为( )m3.
| A、14 | ||
| B、15 | ||
C、14+
| ||
D、15+
|
已知a∈R,则“a=-1”是“a2-1+(a-1)i为纯虚数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |