题目内容
已知集合A={x|x=a0+a1×3+a2×32+a3×33},其中ai∈{1,2,3}(i=0,1,2,3}且a3≠0,则A中所有元素之和等于( )
| A、3 240 |
| B、3 120 |
| C、2 997 |
| D、2 889 |
考点:计数原理的应用,数列的求和
专题:综合题,排列组合
分析:由题意可知a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法,利用数列求和即可求得A中所有元素之和.
解答:
解:由题意可知,a0,a1,a2各有3种取法(均可取0,1,2),a3有2种取法(可取1,2),由分步计数原理可得共有3×3×3×2种方法,
∴当a0取0,1,2时,a1,a2各有3种取法,a3有2种取法,共有3×3×2=18种方法,即集合A中含有a0项的所有数的和为(0+1+2)×18;
同理可得集合A中含有a1项的所有数的和为(3×0+3×1+3×2)×18;
集合A中含有a2项的所有数的和为(32×0+32×1+32×2)×18;
集合A中含有a3项的所有数的和为(33×1+33×2)×27;
由分类计数原理得集合A中所有元素之和:
S=(0+1+2)×18+(3×0+3×1+3×2)×18+(32×0+32×1+32×2)×18+(33×1+33×2)×27
=18(3+9+27)+81×27=702+2 187=2 889.
故选D.
∴当a0取0,1,2时,a1,a2各有3种取法,a3有2种取法,共有3×3×2=18种方法,即集合A中含有a0项的所有数的和为(0+1+2)×18;
同理可得集合A中含有a1项的所有数的和为(3×0+3×1+3×2)×18;
集合A中含有a2项的所有数的和为(32×0+32×1+32×2)×18;
集合A中含有a3项的所有数的和为(33×1+33×2)×27;
由分类计数原理得集合A中所有元素之和:
S=(0+1+2)×18+(3×0+3×1+3×2)×18+(32×0+32×1+32×2)×18+(33×1+33×2)×27
=18(3+9+27)+81×27=702+2 187=2 889.
故选D.
点评:本题考查数列的求和,考查分类计数原理与分步计数原理的应用,考查分类讨论与转化思想的综合应用,属于难题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
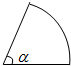 现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )
现要用篱笆围成一个面积为S扇形菜园(如图所示),问要使这个菜园所用篱笆最短,则这个扇形的半径和圆心角各为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
已知向量
与
的夹角为θ,|
|=2,|
|=1,
=t
,
=(1-t)
,|
|在t0时取得最小值.当0<t0<
时,夹角θ的取值范围为( )
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OQ |
| OB |
| PQ |
| 1 |
| 5 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(0,
|
已知|
|=4,
是单位向量,向量
与
的夹角是
,则|
+
|=( )
| a |
| e |
| a |
| e |
| 3π |
| 4 |
| a |
| 2 |
| e |
A、2
| ||
B、4+
| ||
C、
| ||
D、
|
对于平面α和两直线m、n,下列表述正确的是( )
| A、m?α,n?α,则m,n相交 |
| B、若m∥α,m∥n,则n∥α |
| C、若m?α,n∥α,则m∥n |
| D、若m∥α,则m平行于α内的无数条直线 |
函数f(x)=
的定义域为R,则实数a的取值范围是( )
| 1 |
| ax2+4ax+3 |
A、[0,
| ||
B、(0,
| ||
C、(
| ||
| D、(-∞,0) |
某厂生产产品x件的总成本c(x)=1200+
x3(万元),已知产品单价P(万元)与产品件数x满足:P2=
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?( )
| 2 |
| 75 |
| k |
| x |
| A、23 | B、24 | C、25 | D、26 |
已知函数f(x)=lg
,若f(a)=b(b≠0),则f(-a)等于( )
| 1-x |
| 1+x |
| A、-b | ||
| B、b | ||
C、
| ||
D、-
|