题目内容
已知函数f(x)=ax-lnx-1,若曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(Ⅰ)求实数a的值;
(Ⅱ)函数g(x)=f(x)-m(x-1)(m∈R)恰有两个零点x1,x2(x1<x2).
(i)求函数g(x)的单调区间及实数m的取值范围;
(ii)求证:g′(
)>0.
(Ⅰ)求实数a的值;
(Ⅱ)函数g(x)=f(x)-m(x-1)(m∈R)恰有两个零点x1,x2(x1<x2).
(i)求函数g(x)的单调区间及实数m的取值范围;
(ii)求证:g′(
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)求导函数,利用曲线y=f(x)在点(1,f(1))处的切线平行于x轴,即可求实数a的值;
(Ⅱ)(i)求导函数,分类讨论,利用函数g(x)=f(x)-m(x-1)(m∈R)恰有两个零点x1,x2(x1<x2),可得求函数g(x)的单调区间及实数m的取值范围;
(ii)由函数g(x)有两个零点x1,x2(x1<x2),可得
,两式相减,再用分析法,即可证明.
(Ⅱ)(i)求导函数,分类讨论,利用函数g(x)=f(x)-m(x-1)(m∈R)恰有两个零点x1,x2(x1<x2),可得求函数g(x)的单调区间及实数m的取值范围;
(ii)由函数g(x)有两个零点x1,x2(x1<x2),可得
|
解答:
(Ⅰ)解:由f′(x)=a-
,且f'(1)=0,…(2分)
解得a=1.…(3分)
(Ⅱ)(i)解:g(x)=(1-m)(x-1)-lnx,x∈(0,+∞).
令g′(x)=1-m-
=
,…(4分)
当1-m≤0即m≥1时,g'(x)<0,
所以g(x)在(0,+∞)上单调递减,此时只存在一个零点,不合题意;…(5分)
当m<1时,令g'(x)=0,解得x=
.
当x变化时,g(x)和g'(x)变化情况如下表:
 …(6分)
…(6分)
由题意可知,g(x)极小=g(
)=m+ln(1-m).
设h(m)=m+ln(1-m),
当m=0时,h(0)=0即g(x)极小=0,此时g(x)恰有一个零点,不合题意;…(7分)
当m≠0且m<1时,h′(m)=1-
=
,…(8分)
当m<0时,h'(x)>0,当0<m<1时,h'(x)<0
所以h(m)在(-∞,0)上单调递增,在(0,1)上单调递减,
所以h(m)<h(0)=0,此时g(x)恰有两个零点.
综上,m的取值范围是(-∞,0)∪(0,1).…(9分)
(ii)证明:因为函数g(x)有两个零点x1,x2(x1<x2),
所以
,
两式相减得(1-m)(x2-x1)-ln
=0,所以1-m=
ln
.…(10分)
要证g′(
)>0,
只要证1-m-
>0,只要证
ln
-
>0,
只要证ln
-
>0,…(11分)
只要证ln
-
>0.…(12分)ks5u
设φ(t)=lnt-
(t>1),则φ′(t)=
>0,φ(t)在(1,+∞)上单调递增,…(13分)
所以φ(t)>φ(1)=0,
所以g′(
)>0.…(14分)
| 1 |
| x |
解得a=1.…(3分)
(Ⅱ)(i)解:g(x)=(1-m)(x-1)-lnx,x∈(0,+∞).
令g′(x)=1-m-
| 1 |
| x |
| (1-m)x-1 |
| x |
当1-m≤0即m≥1时,g'(x)<0,
所以g(x)在(0,+∞)上单调递减,此时只存在一个零点,不合题意;…(5分)
当m<1时,令g'(x)=0,解得x=
| 1 |
| 1-m |
当x变化时,g(x)和g'(x)变化情况如下表:
 …(6分)
…(6分)由题意可知,g(x)极小=g(
| 1 |
| 1-m |
设h(m)=m+ln(1-m),
当m=0时,h(0)=0即g(x)极小=0,此时g(x)恰有一个零点,不合题意;…(7分)
当m≠0且m<1时,h′(m)=1-
| 1 |
| 1-m |
| -m |
| 1-m |
当m<0时,h'(x)>0,当0<m<1时,h'(x)<0
所以h(m)在(-∞,0)上单调递增,在(0,1)上单调递减,
所以h(m)<h(0)=0,此时g(x)恰有两个零点.
综上,m的取值范围是(-∞,0)∪(0,1).…(9分)
(ii)证明:因为函数g(x)有两个零点x1,x2(x1<x2),
所以
|
两式相减得(1-m)(x2-x1)-ln
| x2 |
| x1 |
| 1 |
| x2-x1 |
| x2 |
| x1 |
要证g′(
| x1+x2 |
| 2 |
只要证1-m-
| 2 |
| x1+x2 |
| 1 |
| x2-x1 |
| x2 |
| x1 |
| 2 |
| x1+x2 |
只要证ln
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
只要证ln
| x2 |
| x1 |
2(
| ||
|
设φ(t)=lnt-
| 2(t-1) |
| t+1 |
| (t-1)2 |
| t(t+1)2 |
所以φ(t)>φ(1)=0,
所以g′(
| x1+x2 |
| 2 |
点评:本小题主要考查函数、函数与导数等基础知识,考查推理论证能力,运算求解能力,考查函数与方程的思想,数形结合的思想,化归与转化思想.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
已知△ABC外接圆的半径为1,圆心为O,且
+
=2
,|
|=|
|,则
•
的值是( )
| CA |
| BA |
| OA |
| OA |
| AB |
| CA |
| BC |
| A、3 | B、2 | C、-2 | D、-3 |
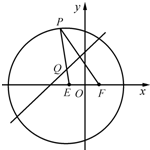 如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+1)2+y2=16,点F(1,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.