题目内容
 已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,
已知函数f(x)是定义域为R的奇函数,当x>0时,f(x)=x2-2x,(1)求f(-2);
(2)求出函数f(x)在R上的解析式;
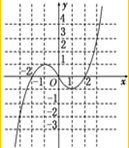
(3)在坐标系中画出函数f(x)的图象.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数的图象
专题:函数的性质及应用
分析:(1)由题意f(-2)=-f(2),问题可解;
(2)先求出x≤0时的解析式,然后即可得到函数在定义域上的解析式(分段函数);
(3)根据二次函数图象的画法求解.
(2)先求出x≤0时的解析式,然后即可得到函数在定义域上的解析式(分段函数);
(3)根据二次函数图象的画法求解.
解答:
解:(1)由于函数是定义在(-∞,+∞)上的奇函数,
因此对任意的x都有f(-x)=-f(x)
∴f(-2)=-f(2),而f(2)=22-2×2=0,∴f(-2)=0;
(2)①由于函数f(x)是定义域为R的奇函数,则f(0)=0;
②当x<0时,-x>0,∵f(x)是奇函数,∴f(-x)=-f(x).
∴f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x.
综上:f(x)=
;
(3)图象如下图:
因此对任意的x都有f(-x)=-f(x)
∴f(-2)=-f(2),而f(2)=22-2×2=0,∴f(-2)=0;
(2)①由于函数f(x)是定义域为R的奇函数,则f(0)=0;
②当x<0时,-x>0,∵f(x)是奇函数,∴f(-x)=-f(x).
∴f(x)=-f(-x)=-[(-x)2-2(-x)]=-x2-2x.
综上:f(x)=
|
(3)图象如下图:

点评:本题考查了函数的奇偶性以及二次函数图象的画法,属于基础题,难度不大.

练习册系列答案
相关题目
已知f(x),g(x)分别为定义在R上的奇函数和偶函数,且f(x)-g(x)=x2-x+3,则f(1)+g(1)=( )
| A、5 | B、-5 | C、3 | D、-3 |
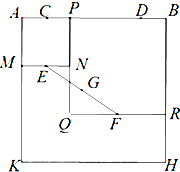 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为