题目内容
14.函数f(x)=2sin(ωx-$\frac{π}{6}$)-1最小正周期是π,则函数f(x)的单调递增区间是[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.分析 利用正弦函数的周期性求得ω,再利用正弦函数的单调性求得f(x)的单调递增区间.
解答 解:∵函数f(x)=2sin(ωx-$\frac{π}{6}$)-1最小正周期是$\frac{2π}{ω}$=π,∴ω=2,则函数f(x)=2sin(2x-$\frac{π}{6}$)-1.
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,可得函数的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z,
故答案为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
点评 本题主要考查正弦函数的周期性和单调性,属于基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
15.若x=1是函数f(x)=$\frac{a}{x}$+b(a≠0)的一个零点,则函数h(x)=ax2+bx的零点是( )
| A. | 0或-1 | B. | 0或-2 | C. | 0或1 | D. | 0或2 |
2.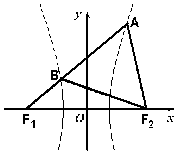 如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )
如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )
 如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )
如图,F1、F2分别是双曲线的左、右焦点,过F1的直线与双曲线的左、右两支分别相交于B、A两点,若△ABF2为等边三角形,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{7}$ | D. | 3 |
19.已知F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,过F1的直线l与双曲线的左右两支分别交于点A、B,若△ABF2是以∠ABF2为顶点的等腰直角三角形,则双曲线的离心率的平方为( )
| A. | 5+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | $\sqrt{7}$ | D. | 3+2$\sqrt{2}$ |
6.已知函数f(x)=ax-1(a>0,且a≠1)满足f(1)>1,若函数g(x)=f(x+1)-4的图象不过第二象限,则a的取值范围是( )
| A. | (2,+∞) | B. | (2,5] | C. | (1,2) | D. | (1,5] |
3.若函数f(2x+1)的定义域为(-1,0),则函数f(x)的定义域为( )
| A. | (-2,0) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
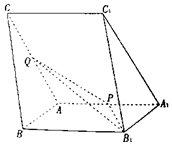 如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点.
如图,三棱柱ABC-A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1,AC的中点. 如图,直角梯形OABC中,∠COA=∠OAB=$\frac{π}{2}$,OC=2,OA=AB=1,SO⊥平面OABC,且SO=1,点M为SC的中点.
如图,直角梯形OABC中,∠COA=∠OAB=$\frac{π}{2}$,OC=2,OA=AB=1,SO⊥平面OABC,且SO=1,点M为SC的中点.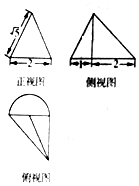 某几何体上的三视图如图所示,则该几何体的体积是$\frac{4+π}{3}$.
某几何体上的三视图如图所示,则该几何体的体积是$\frac{4+π}{3}$.