题目内容
6.已知函数f(x)=ax-1(a>0,且a≠1)满足f(1)>1,若函数g(x)=f(x+1)-4的图象不过第二象限,则a的取值范围是( )| A. | (2,+∞) | B. | (2,5] | C. | (1,2) | D. | (1,5] |
分析 利用指数函数的单调性可得a>2.由于函数g(x)=ax+1-5的图象不过第二象限,可得g(0)≤0,求解即可得答案.
解答 解:∵f(1)>1,
∴a-1>1,
即a>2
∵函数g(x)=f(x+1)-4的图象不过第二象限,
∴g(0)=a1-1-4≤0,
∴a≤5,
∴a的取值范围是(2,5].
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了数学转化思想方法,考查推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在长方体ABCD-A1B1C1D1中,底面ABCD的边长为a的正方形,E是CC1的中点,若该长方体的外接球的表面积为10πa2,则异面直线AE与C1D1所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
11.已知点M的坐标(x,y)满足不等式组$\left\{\begin{array}{l}{2x+y-4≥0}\\{x-y-2≤0}\\{y-3≤0}\end{array}\right.$,N为直线y=-2x+2上任一点,则|MN|的最小值是( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 1 | D. | $\frac{\sqrt{17}}{2}$ |
18.表面积为3π的圆锥的侧面展开图是一个半圆,则该圆锥的底面圆半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.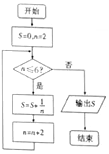 如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.
如图所示的程序框图中,输出的S的值为$\frac{11}{12}$.