题目内容
函数f（x）=log2（x+1）+
的定义域为（ ）
| 4-x2 |
| A、（-1，2] |
| B、（-1，2） |
| C、[-1，2） |
| D、[-1，2] |
考点：对数函数的定义域
专题：函数的性质及应用
分析：根据函数成立的条件，建立不等式关系即可得到结论．
解答：
解：要使函数有意义，则
，
即
，
∴-1＜x≤2，
故函数的定义域为（-1，2]，
故选：A．
|
即
|
∴-1＜x≤2，
故函数的定义域为（-1，2]，
故选：A．
点评：本题主要考查函数定义域的求法，利用函数成立的条件是解决本题的关键，比较基础．
练习册系列答案
相关题目
| ∫ | 0 -2 |
| 4-x2 |
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
设f（x）=xex，若f′（xo）=0，则x0等于（ ）
| A、e2 | ||
| B、-1 | ||
C、
| ||
| D、ln2 |
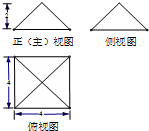
某几何体的三视图如图所示，则该几何体的体积是（ ）
| A、32 | ||||
B、
| ||||
C、
| ||||
D、
|
设函数f（x）可导，则
等于（ ）
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′（15） | ||
| B、3f′（15） | ||
C、
| ||
| D、f′（3） |
要得到函数y=cos（2x+
）的图象，只需将y=cos2x的图象（ ）
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
下列不等式成立的是（ ）
| A、ex＜x+1 | ||||
| B、lnx＞x-1 | ||||
C、sinx＜
| ||||
D、sinx＞
|