题目内容
函数f(x)=x2cosx在x=
处的导数值等于 .
| π |
| 2 |
考点:导数的运算
专题:导数的概念及应用
分析:求函数的导数,根据导数的运算法则即可得到结论.
解答:
解:由导数的运算法则可知f′(x)=2xcosx-x2sinx,
∴f′(
)=2×
cos
-(
)2sin
=-
,
故答案为:-
∴f′(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π2 |
| 4 |
故答案为:-
| π2 |
| 4 |
点评:本题主要考查导数的基本计算,要求熟练掌握函数的导数公式以及导数的运算法则,比较基础.

练习册系列答案
相关题目
已知定义在R上的奇函数f(x)满足f(x+2e)=-f(x)(其中e为自然对数的底),且在区间[e,2e]上是减函数,又a=lg6,b=log23,(
)c-2<1且lnc<1,则有( )
| 1 |
| 2 |
| A、f(a)<f(b)<f(c) |
| B、f(b)<f(c)<f(a) |
| C、f(c)<f(a)<f(b) |
| D、f(c)<f(b)<f(a) |
△ABC中,A,B为锐角,a,b,c为其三边长,如果asinA+bsinB=c,则∠C的大小为( )
| A、30° | B、45° |
| C、60° | D、90° |
由点P(4,3)引圆x2+y2=9的切线,则切线的长为( )
| A、5 | B、4 | C、3 | D、2 |
设函数f(x)可导,则
等于( )
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′(15) | ||
| B、3f′(15) | ||
C、
| ||
| D、f′(3) |
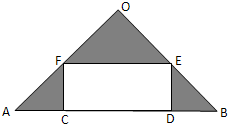 为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=
为响应党的十八大提出的文化强国建设的号召,某县政府计划建立一个文化产业园区,计划在等腰三角形OAB的空地上修建一个占地面积为S的矩形CDEF文化园展厅,如图点C、D在底边AB上,E、F分别在腰OB、OA上,已知OA=OB=30米,AB=