题目内容
16.已知曲线C的极坐标方程为ρ=2cosθ.以极点为原点,极轴为x轴的正半轴建立直角坐标系,则曲线C的直角坐标方程为x2+y2-2x=0.分析 利用公式ρ2=x2+y2,x=ρcosθ化简曲线C的方程,可得它的直角坐标方程.
解答 解:由ρ=2cosθ,两边同时乘以ρ得ρ2=2ρcosθ,
即 x2+y2=2x,∴x2+y2-2x=0.
故答案为:x2+y2-2x=0.
点评 本题考查把曲线的极坐标化为直角坐标方程的方法,熟记极坐标化直角坐标的公式是关键,属于基础题.

练习册系列答案
相关题目
1.点(0,0)和点(-1,1)在直线2x+y+m=0的同侧,则m的取值范围是( )
| A. | m>1或m<0 | B. | m>2或m<1 | C. | 0<m<1 | D. | 1<m<2 |
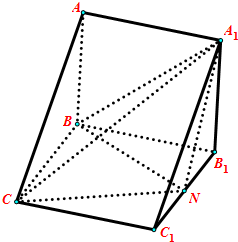 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.