题目内容
设斜率为
的直线l与双曲线
-
=1(a>0,b>0)交于不同的两点P、Q,若点P、Q在x轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是( )
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设斜率为
的直线l:y=
x+t,代入双曲线方程,消去y,由题意可得,方程的两根分别为-c,c.则有t=0,代入c,得到方程,再由a,b,c的关系和离心率公式,计算即可得到所求.
| ||
| 2 |
| ||
| 2 |
解答:
解:设斜率为
的直线l:y=
x+t,
代入双曲线方程,消去y,可得,(b2-
a2)x2-
a2tx-a2t2-a2b2=0,
由于点P、Q在x轴上的射影恰好为双曲线的两个焦点,
则有上式的两根分别为-c,c.
则t=0,即有(b2-
a2)c2=a2b2,由于b2=c2-a2,
则有2c4-5a2c2+2a4=0,由e=
,则2e4-5e2+2=0,
解得e2=2(
舍去),
则e=
.
故选:A.
| ||
| 2 |
| ||
| 2 |
代入双曲线方程,消去y,可得,(b2-
| 1 |
| 2 |
| 2 |
由于点P、Q在x轴上的射影恰好为双曲线的两个焦点,
则有上式的两根分别为-c,c.
则t=0,即有(b2-
| 1 |
| 2 |
则有2c4-5a2c2+2a4=0,由e=
| c |
| a |
解得e2=2(
| 1 |
| 2 |
则e=
| 2 |
故选:A.
点评:本题考查双曲线的方程和性质,考查直线方程和双曲线方程联立,消去未知数,运用韦达定理,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
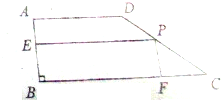 有一块形状为直角梯形的材料ABCD,底边BC的长为5米,边AB的长为1米(其中0<t<
有一块形状为直角梯形的材料ABCD,底边BC的长为5米,边AB的长为1米(其中0<t<