题目内容
16.射洪县教育局从去年参加了计算机职称考试,并且年龄在[25,55]岁的教师中随机抽取n人的成绩进行了调查,得到如下统计表和各年龄段人数频率分布直方图: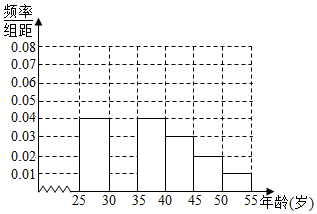
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
(2)若用以上数据来估计今年参考老师的过关情况,并将每组的频率视作对应年龄阶段老师的过关概率,考试是否过关互不影响.现有三名教师参加该次考试,年龄分别为41岁、47岁、53岁.记ξ为过关的人数,请利用相关数据求ξ的分布列和数学期望.
分析 (1)根据频率和为1,计算[30,35)内的频率,求出对应小矩形的高,
补全频率分布直方图,计算样本容量n以及p、a和q的值;
(2)求出年龄分别为41岁、47岁、53岁过关的概率,
得ξ的可能取值,求出对应的概率值,写出ξ的分布列,计算数学期望值.
解答 解:(1)根据频率和为1,得[30,35)内的频率为
1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
∴$\frac{0.3}{5}$=0.06,
∴补全频率分布直方图如图所示: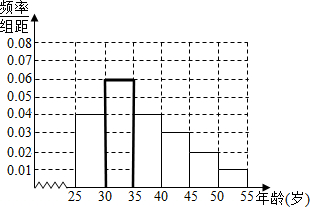
第一组的人数为$\frac{120}{0.6}$=200,频率为0.04×5=0.2,
∴n=$\frac{200}{0.2}$=1000;
第二组的频率为0.3,
∴第二组的人数为1000×0.3=300,
∴p=$\frac{195}{300}$=0.65;
第四组共有1000×0.15=150人,
∴a=150×0.4=60;
第五组共有1000×0.1=100人,
∴q=30÷100=0.3;
综上,a=60,p=0.65,q=0.3;
(2)根据题意,年龄分别为41岁、47岁、53岁过关的概率分别为$\frac{2}{5}$,$\frac{3}{10}$,$\frac{3}{10}$,
则P(ξ=0)=$\frac{3}{5}$×$\frac{7}{10}$×$\frac{7}{10}$=$\frac{147}{500}$,P(ξ=1)=$\frac{2}{5}$×$\frac{7}{10}$×$\frac{7}{10}$+2×$\frac{3}{5}$×$\frac{3}{10}$×$\frac{7}{10}$=$\frac{224}{500}$,
P(ξ=2)=2×$\frac{2}{5}$×$\frac{3}{10}$×$\frac{7}{10}$+$\frac{3}{5}$×$\frac{3}{10}$×$\frac{3}{10}$=$\frac{111}{500}$,
P(ξ=3)=$\frac{2}{5}$×$\frac{3}{10}$×$\frac{3}{10}$=$\frac{18}{500}$;
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{147}{500}$ | $\frac{224}{500}$ | $\frac{111}{500}$ | $\frac{18}{500}$ |
点评 本题考查了频率分布直方图的应用问题,也考查了离散型随机变量的分布列与数学期望的计算问题,是综合题.

| A. | (-2,+∞) | B. | (2,+∞) | C. | (1,+∞) | D. | (0,+∞) |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |