题目内容
7.设x∈R,向量$\overrightarrow a=(x,1)$,$\overrightarrow b=(1,-2)$,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$|{\overrightarrow a+2\overrightarrow b}|$=5.分析 根据题意,由$\overrightarrow{a}$⊥$\overrightarrow{b}$,分析可得$\overrightarrow{a}$•$\overrightarrow{b}$=x-2=0,解可得x的值,即可得$\overrightarrow{a}$的坐标,由向量的坐标计算公式可得$\overrightarrow{a}$+2$\overrightarrow{b}$的坐标,由向量模的公式计算可得答案.
解答 解:根据题意,向量$\overrightarrow a=(x,1)$,$\overrightarrow b=(1,-2)$,
若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则有$\overrightarrow{a}$•$\overrightarrow{b}$=x-2=0,
解可得x=2,故$\overrightarrow{a}$=(2,1),
又由$\overrightarrow b=(1,-2)$,则$\overrightarrow{a}$+2$\overrightarrow{b}$=(4,3),
则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{9+16}$=5;
故答案为:5
点评 本题 考查向量的坐标运算,关键是求出向量$\overrightarrow{a}$+2$\overrightarrow{b}$的坐标.

练习册系列答案
相关题目
12. 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{11}$ | D. | $\frac{4}{13}$ |
16.射洪县教育局从去年参加了计算机职称考试,并且年龄在[25,55]岁的教师中随机抽取n人的成绩进行了调查,得到如下统计表和各年龄段人数频率分布直方图: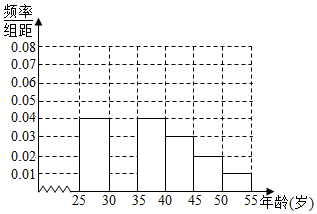
(1)补全频率分布直方图,并求a、p、q的值;
(2)若用以上数据来估计今年参考老师的过关情况,并将每组的频率视作对应年龄阶段老师的过关概率,考试是否过关互不影响.现有三名教师参加该次考试,年龄分别为41岁、47岁、53岁.记ξ为过关的人数,请利用相关数据求ξ的分布列和数学期望.

| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
(2)若用以上数据来估计今年参考老师的过关情况,并将每组的频率视作对应年龄阶段老师的过关概率,考试是否过关互不影响.现有三名教师参加该次考试,年龄分别为41岁、47岁、53岁.记ξ为过关的人数,请利用相关数据求ξ的分布列和数学期望.
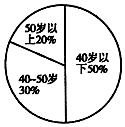 200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人.
200名职工年龄分布如图所示,从中随机抽取40名职工作样本,采用系统抽样方式,按1~200编号分为40组,分别为1~5,6~10,…,196~200,第5组抽取号码为23,第9组抽取号码为43;若采用分层抽样,40-50岁年龄段应抽取12人. 某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元)
某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元)