题目内容
1.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为单位向量且夹角为$\frac{π}{3}$,设$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{2}}$,$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$\frac{3}{2}$.分析 可知$|\overrightarrow{{e}_{1}}|=|\overrightarrow{{e}_{2}}|=1$,且$<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>=\frac{π}{3}$,这样即可求出$\overrightarrow{a}•\overrightarrow{b}$及$|\overrightarrow{b}|$的值,从而得出$\overrightarrow{a}$在$\overrightarrow{b}$方向上投影的值.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=(\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{2}}$
=$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{\overrightarrow{{e}_{2}}}^{2}$
=$\frac{1}{2}+1$
=$\frac{3}{2}$,且$|\overrightarrow{b}|=1$;
∴$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为:
$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=|\overrightarrow{a}|•\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 考查单位向量及投影的定义,数量积的运算及计算公式.

 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{11}$ | D. | $\frac{4}{13}$ |
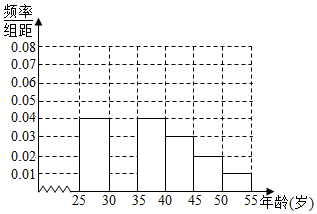
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
(2)若用以上数据来估计今年参考老师的过关情况,并将每组的频率视作对应年龄阶段老师的过关概率,考试是否过关互不影响.现有三名教师参加该次考试,年龄分别为41岁、47岁、53岁.记ξ为过关的人数,请利用相关数据求ξ的分布列和数学期望.
| A. | 29 | B. | 30 | C. | 31 | D. | 33 |
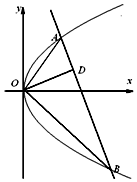 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).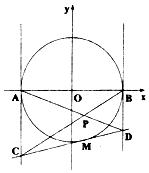 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.