题目内容
2.设f(x)=(x-1)3+x+2,{an}是公差为$\frac{1}{2}$的等差数列,且f(a1)+f(a2)+f(a3)+f(a4)+f(a5)+f(a6)=18,则a1=( )| A. | -$\frac{1}{4}$ | B. | -$\frac{7}{4}$ | C. | -$\frac{5}{4}$ | D. | -$\frac{3}{4}$ |
分析 由已知函数解析式构造新函数g(x)=f(x)-3,可得g(x)关于(1,0)对称.把f(a1)+f(a2)+f(a3)+f(a4)+f(a5)+f(a6)=18变形可得g(a1)+g(a2)+…+g(a6)=0,即g(a3)与g(a4)关于(1,0)对称,由对称性得到a3+a4=2,再结合已知求得a1.
解答 解:∵f(x)=(x-1)3+x+2,∴f(x)-3=(x-1)3+x-1,
令g(x)=f(x)-3,
∴g(x)关于(1,0)对称.
∵f(a1)+f(a2)+…+f(a6)=18,
∴f(a1)-3+f(a2)-3+…+f(a6)-3=0,
∴g(a1)+g(a2)+…+g(a6)=0,
∴g(a3)与g(a4)关于(1,0)对称,
则a3+a4=$2{a}_{1}+5d=2{a}_{1}+\frac{5}{2}=2$.
解得:${a}_{1}=-\frac{1}{4}$.
故选:A.
点评 本题考查等差数列的通项公式,考查了数列的函数特性,训练了函数构造法,灵活性强,难度较大.

练习册系列答案
相关题目
12.在数列{xn}中,x1=8,x4=2,且满足xn+2+xn=2xn+1,n∈N+.则x10=( )
| A. | -10 | B. | 10 | C. | -20 | D. | 20 |
7.已知点P(2,2)在直线l:Ax+By+C=0上,则方程Bx-Ay+4A+C=0是( )
| A. | 不过点P且与l垂直的直线 | B. | 不过点P且与l平行的直线 | ||
| C. | 过点P且与l垂直的直线 | D. | 过点P且与l平行的直线 |
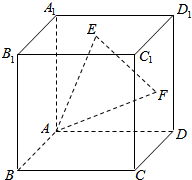 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量: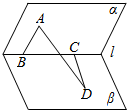 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.