题目内容
20.实数k满足y=(1-k2)x+3k+4在R上是单调增函数,k取值构成集合A,奇函数f(x)是定义在A上的单调减函数,若f(a-1)+f(2a-1)>0.求实数a的取值范围.分析 由一次函数的单调性,可得k的范围,即集合A,进而根据函数的奇偶性和单调性,可将不等式f(a-1)+f(2a-1)>0化为:-1<a-1<-2a+1<1,解得实数a的取值范围.
解答 解:若y=(1-k2)x+3k+4在R上是单调增函数,
则1-k2>0,解得:k∈(-1,1),
故A=(-1,1),
若奇函数f(x)是定义在A上的单调减函数,
则不等式f(a-1)+f(2a-1)>0可化为:f(a-1)>-f(2a-1)
即f(a-1)>f(-2a+1),
即-1<a-1<-2a+1<1,
解得:a∈(0,$\frac{2}{3}$)
点评 本题考查的知识点是函数单调性的性质,函数奇偶性的性质,难度中档.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
5.设a,b∈R,命题“若a>1且b>1,则a+b>2”的逆否命题是( )
| A. | 若a≤1且b≤1,则a+b≤2 | B. | 若a≤1或b≤1,则a+b≤2 | ||
| C. | 若a+b≤2,则a≤1且b≤1 | D. | 若a+b≤2,则a≤1或b≤1 |
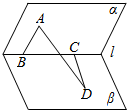 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.