题目内容
16.抛物线x2=-2y与过点P(0,-1)的直线l交于A,B两点,如果OA与OB的斜率之和为1,则直线l的方程是( )| A. | y=-x-1 | B. | y=x+1 | C. | y=x-1 | D. | y=-x+1 |
分析 由题意可得设直线l的方程为y=kx-1,联立直线与抛物线的方程可得:x2+2kx-2=0,根据韦达定理可得答案.
解答 解:由题意可得直线l的斜率存在,设直线l的方程为y=kx-1,A(x1,y1),B(x2,y2),
所以联立直线与抛物线x2=-2y可得:x2+2kx-2=0,
所以x1+x2=-2k,x1x2=-2,
因为OA和OB的斜率之和为1,即 $\frac{{y}_{1}}{{x}_{1}}$+$\frac{{y}_{2}}{{x}_{2}}$=1,
所以 $\frac{{kx}_{1}-1}{{x}_{1}}$+$\frac{{kx}_{2}-1}{{x}_{2}}$=2k-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=1,
所以k=1,
所以直线l的方程为y=x-1.
故选:C.
点评 本题主要考查抛物线的简单性质、直线的一般式方程、直线与抛物线的位置关系,以及方程思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1的离心率e=$\frac{1}{2}$,则m的值为( )
| A. | 3 | B. | 1 | C. | 16或1 | D. | $\frac{16}{3}$或3 |
5.设a,b∈R,命题“若a>1且b>1,则a+b>2”的逆否命题是( )
| A. | 若a≤1且b≤1,则a+b≤2 | B. | 若a≤1或b≤1,则a+b≤2 | ||
| C. | 若a+b≤2,则a≤1且b≤1 | D. | 若a+b≤2,则a≤1或b≤1 |
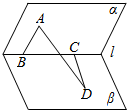 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.