题目内容
3个单位从4名大学毕业生中选聘工作人员,若每个单位至少选聘1人(4名大学毕业生不一定都能选聘上),则不同的选聘方法种数为 .(用具体数字作答)
考点:计数原理的应用
专题:应用题,排列组合
分析:分类讨论:选用3名大学生:
,4名大学毕业生都能选聘上:
,利用加法原理可得结论.
| C | 3 4 |
| A | 3 3 |
| C | 2 4 |
| A | 3 3 |
解答:
解:分类讨论:
选用3名大学生:
=24种;
4名大学毕业生都能选聘上:
=36种,
故共有24+36=60种.
故答案为:60.
选用3名大学生:
| C | 3 4 |
| A | 3 3 |
4名大学毕业生都能选聘上:
| C | 2 4 |
| A | 3 3 |
故共有24+36=60种.
故答案为:60.
点评:本题考查计数原理的应用,考查分类讨论的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为P1,P2,P3,则( )
| A、P1=P2<P3 |
| B、P2=P3<P1 |
| C、P1=P3<P2 |
| D、P1=P2=P3 |
执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )


| A、[-6,-2] |
| B、[-5,-1] |
| C、[-4,5] |
| D、[-3,6] |
已知向量
=(1,
),
=(3,m),若向量
,
的夹角为
,则实数m=( )
| a |
| 3 |
| b |
| a |
| b |
| π |
| 6 |
A、2
| ||
B、
| ||
| C、0 | ||
D、-
|
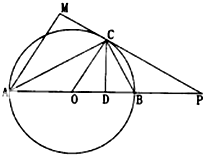 如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D.
如图,已知AB是⊙O的直径,C为⊙O上一点,以C为切点的切线交AB的延长线于点P,AM⊥CP,垂足为M,CD⊥AB,垂足为D. 高三(2)班在一次数学考试中,对甲、乙两组各12名同学的成绩进行统计分析,两组成绩的茎叶图如图所示,成绩不少于90分为及格,现从两组成绩中按分层抽样抽取一个容量为6的样本,则不及格分数应抽
高三(2)班在一次数学考试中,对甲、乙两组各12名同学的成绩进行统计分析,两组成绩的茎叶图如图所示,成绩不少于90分为及格,现从两组成绩中按分层抽样抽取一个容量为6的样本,则不及格分数应抽