题目内容

已知向量
a
=（1，
3
），
b
=（3，m），若向量
a
，
b
的夹角为
π
6
，则实数m=（　　）
A、2
3
B、
3
C、0
D、-
3
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由条件利用两个向量的夹角公式、两个向量的数量积公式，求得m的值．
解答： 解：由题意可得cos
π
6
=
a
•
b
|
a
|•|
b
|
=
3+ 
3
 m
2
9+m2
=
3
2
，
解得 m=
3
，
故选：B．
点评：本题主要考查两个向量的夹角公式、两个向量的数量积公式的应用，属于基础题．
练习册系列答案
相关题目
3个单位从4名大学毕业生中选聘工作人员，若每个单位至少选聘1人（4名大学毕业生不一定都能选聘上），则不同的选聘方法种数为
 
．（用具体数字作答）
已知a＞b＞0，椭圆C1的方程为
x2
a2
+
y2
b2
=1，双曲线C2的方程为
x2
a2
-
y2
b2
=1，C1与C2的离心率之积为
3
2
，则C2的渐近线方程为（　　）
A、x±
2
y=0
B、
2
x±y=0
C、x±2y=0
D、2x±y=0
如图所示，程序框图（算法流程图）的输出结果是（　　）
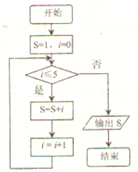
A、11B、15C、16D、22
如图所示，程序框图（算法流程图）的输出结果是（　　）
A、22B、16C、15D、11
已知四棱锥P-ABCD，现要在四棱锥的各个面上涂色，有4种不同的颜色可供选择，要求相邻的面不同色，则不同的涂色方法有（　　）种．
A、60B、120C、48D、72
设{an}的首项为a1，公差为-1的等差数列，Sn为其前n项和，若S1，S2，S4成等比数列，则a1=（　　）
A、2
B、-2
C、
1
2
D、-
1
2
已知0＜a＜1，求证：
1
a
+
4
1-a
≥9．
已知等差数列{an}的前n项和Sn，a5=5，S5=15，则数列{
1
anan+1
}的前2014项的和为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网