题目内容
已知
=(-1,
),|
|=log4|
|,若(
-2
)⊥
,则向量
与
的夹角是( )
| a |
| 3 |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
| A、60° | B、30° |
| C、120° | D、150° |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由已知得|
|=
=2,|
|=log4|
|=
,
•
=2
2=2×
=
,由此得到<
,
>=60°.
| a |
| 1+3 |
| b |
| 4 |
| 1 |
| 2 |
| a |
| b |
| b |
| 1 |
| 4 |
| 1 |
| 2 |
| a |
| b |
解答:
解:∵
=(-1,
),|
|=log4|
|,
∴|
|=
=2,|
|=log4|
|=
,
∵(
-2
)⊥
,
∴
•
=2
2=2×
=
,
∴cos<
,
>=
=
=
,
∴<
,
>=60°.
故选:A.
| a |
| 3 |
| b |
| a |
∴|
| a |
| 1+3 |
| b |
| 4 |
| 1 |
| 2 |
∵(
| a |
| b |
| b |
∴
| a |
| b |
| b |
| 1 |
| 4 |
| 1 |
| 2 |
∴cos<
| a |
| b |
| ||||
|
|
| ||
2×
|
| 1 |
| 2 |
∴<
| a |
| b |
故选:A.
点评:本题考查向量
与
的夹角的求法,是基础题,解题时要注意向量垂直的性质的合理运用.
| a |
| b |

练习册系列答案
相关题目
一空间几何体的三视图如图所示,则该几何体的体积为( )


| A、10 | B、20 | C、30 | D、40 |
设集合A-{1,2,3},B={-1,1},则A∩B=( )
| A、∅ |
| B、{1} |
| C、{-1,1} |
| D、{-1,1,2,3} |
已知双曲线x2+my2=1的虚轴长是实轴长的两倍,则实数m的值是( )
| A、4 | ||
B、-
| ||
C、
| ||
| D、-4 |
记集合M={x|x>2},N={x|x2-3x≤0},则M∩N=( )
| A、{x|2<x≤3} |
| B、{x|x>0或x<-2} |
| C、{x|-2<x≤3} |
| D、{x|0<x<2} |
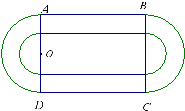 双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.