题目内容
8.设i是虚数单位,复数$\frac{a+i}{1+i}$为纯虚数,则实数a的值为( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
分析 由复数代数形式的乘除运算化简$\frac{a+i}{1+i}$,由整理出实部和虚部,由纯虚数的定义列出方程组,求出a的值.
解答 解:由题意得,$\frac{a+i}{1+i}$=$\frac{(a+i)(1-i)}{(1+i)(1-i)}$=$\frac{a+1+(1-a)i}{2}$
=$\frac{a+1}{2}+\frac{a-1}{2}i$,
因为复数$\frac{a+i}{1+i}$为纯虚数,所以$\left\{\begin{array}{l}{\frac{a+1}{2}=0}\\{\frac{a-1}{2}≠0}\end{array}\right.$,
解得a=-1,
故选A.
点评 本题考查复数代数形式的乘除运算,以及纯复数的定义的应用,属于基础题.

练习册系列答案
相关题目
19.在学期初,某班开展任课教师对特困生的帮扶活动,已知该班有3名青年任课教师与4名特困生结成帮扶关系,若这3名青年教师每位至少与一名学生结成帮扶关系,又这4名特困学生都能且只能得到一名教师的帮扶,那么不同的帮扶方案的种数为( )
| A. | 36 | B. | 72 | C. | 24 | D. | 48 |
3.设$\frac{i}{1+i}$=a+bi(a,b∈R,i为虚数单位),则|a-bi|=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
13.定义在R上的奇函数f(x)满足:f(x+1)=f(x-1),且当-1<x<0时,f(x)=2x-1,则f(log220)等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
18.已知集合$M=\{x|\frac{2x-1}{x+1}≤1\}$,N={x|-1<x<1},则( )
| A. | M?N | B. | N?M | C. | M=N | D. | M∩N=∅ |
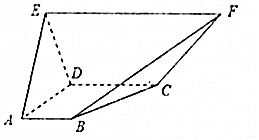 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.