题目内容
18．已知x，y∈R，i是虚数单位．若x+yi与$\frac{3+i}{1+i}$互为共轭复数，则x+y=（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 由复数的乘除运算化简$\frac{3+i}{1+i}$，由共轭复数的定义求出x、y，可得x+y的值．
解答 解：由题意得，$\frac{3+i}{1+i}$=$\frac{（3+i）（1-i）}{（1+i）（1-i）}$=$\frac{4-2i}{2}$=2-i，
因为x+yi与$\frac{3+i}{1+i}$互为共轭复数，
所以x=2、y=1，则x+y=3，
故选D．
点评 本题考查复数代数形式的乘除运算，以及共轭复数的定义的应用，属于基础题．
练习册系列答案
相关题目
9．通过随机询问110名性别不同的大学生是否爱好某处运动，得到如下的列联表：
由卡方公式算得：K2≈7.8
附表：
参照附表：得到的正确的结论是（ ）
| 男 | 女 | 合计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
附表：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A． | 在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别无关” | |
| B． | 在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别有关” | |
| C． | 有99%以上的把握认为“爱好该运动与性别有关” | |
| D． | 有99%以上的把握认为“爱好该运动与性别无关” |
如图，菱形ABCD中，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB=2，CF=3．
7．
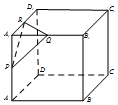正方体ABCD-A1B1C1D1的棱长为a，P，Q，R分别是棱A1A，A1B1，A1D1的中点，以△PQR为底面作直三棱柱（侧棱与底面垂直的三棱柱叫直三棱柱），若此三棱柱另一底面的三个顶点也都在该正方体的表面上，则这个三棱柱的高为（ ）
正方体ABCD-A1B1C1D1的棱长为a，P，Q，R分别是棱A1A，A1B1，A1D1的中点，以△PQR为底面作直三棱柱（侧棱与底面垂直的三棱柱叫直三棱柱），若此三棱柱另一底面的三个顶点也都在该正方体的表面上，则这个三棱柱的高为（ ）| A． | $\frac{{\sqrt{2}}}{2}$a | B． | $\sqrt{2}$a | C． | $\frac{{\sqrt{3}}}{3}$a | D． | $\frac{{\sqrt{3}}}{2}$a |
8．设i是虚数单位，复数$\frac{a+i}{1+i}$为纯虚数，则实数a的值为（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |