Question

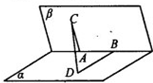如图，在二面角α-AB-β的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，CD=2

17

，则直线CD与平面α所成角的正弦值为（　　）

• A、

  697

  34

• B、

  3 51

  64

• C、

  697

  64

• D、

  3 51

  34

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：由题设条件推导出二面角α-AB-β是60°的二面角，过点C作CF⊥α，交α于F，连结AF，DF，由三垂线定理知∠CAF=60°，CF=6sin60°=3

3

，∠CDF是直线CD与平面α所成角的平面角，由此能求出结果．

解答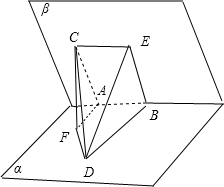： 解：如图，过点C作CE∥AB，过点B作BE∥AC，交CE于点E，
∵在二面角α-AB-β的棱上有A、B两点，
直线AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，
AB=4，AC=6，BD=8，CD=2

17

，
∴ABEC是矩形，∴CE=AB=4，BE=AC=6，
∴CE⊥BE，CE⊥BD，∵BD∩BE=B，∴CE⊥平面BDE，
∵DE?平面BDE，∴CE⊥DE，
∴DE=

CD2-CE2

=

68-16

=2

13

，
∴∠DBE=

82+62-(2 13 )2

2×8×6

=

1

2

，
∴∠DBE=60°，∴二面角α-AB-β是60°的二面角，
过点C作CF⊥α，交α于F，连结AF，DF，
由三垂线定理知∠CAF是二面角α-AB-β的平面角，∴∠CAF=60°，
∴CF=6sin60°=3

3

，
∵CF⊥α，∴∠CDF是直线CD与平面α所成角的平面角，
∴sin∠CDF=

CF

CD

=

3 3

2 17

=

3 51

34

．
故选：D．

点评：本题考查直线与平面所成角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．