题目内容
如图，在△OAB中，P为线段AB上的一点，
=x
+y
，且
=3
，则（ ）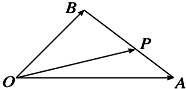
| OP |
| OA |
| OB |
| BP |
| PA |
A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由
=3
，利用向量三角形法则可得
-
=3(
-
)，化为
=
+
，又
=x
+y
，利用平面向量基本定理即可得出．
| BP |
| PA |
| OP |
| OB |
| OA |
| OP |
| OP |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
| OP |
| OA |
| OB |
解答：
解：∵
=3
，
∴
-
=3(
-
)，
化为
=
+
，
又
=x
+y
，
∴x=
，y=
．
故选：D．
| BP |
| PA |
∴
| OP |
| OB |
| OA |
| OP |
化为
| OP |
| 3 |
| 4 |
| OA |
| 1 |
| 4 |
| OB |
又
| OP |
| OA |
| OB |
∴x=
| 3 |
| 4 |
| 1 |
| 4 |
故选：D．
点评：本题考查了向量三角形法则、平面向量基本定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
在正方体ABCD-A1B1C1D1中，动点P在底面ABCD内，且P到棱AD的距离与到面对角线BC1的距离相等，则点P的轨迹是（ ）
| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
“直线l垂直于平面α”的一个必要不充分条件是（ ）
| A、直线l与平面α内的任意一条直线垂直 |
| B、过直线l的任意一个平面与平面α垂直 |
| C、存在平行于直线l的直线与平面α垂直 |
| D、经过直线l的某一个平面与平面α垂直 |
如图，在四棱锥P-ABCD中，底面ABCD是正方形，AC，BD交于点O，PO⊥平面ABCD，PA=AB，E，F，G分别是PO，AD，AB的中点．