题目内容
设集合A={x|(2+x)(3-x)≥0},B={x|f(x)=
,k<0}
(1)求集合A;
(2)若x∈A是x∈B的必要不充分条件,试求实数k的取值范围.
| kx2+4x+k+3 |
(1)求集合A;
(2)若x∈A是x∈B的必要不充分条件,试求实数k的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:集合,简易逻辑
分析:(1)利用一元二次不等式的解法即可得出;
(2)记g(x)=kx2+4x+k+3,由g(x)≥0在R上有解,而k<0,由△≥0,得-4≤k<0,对k分类讨论,及其充要条件的判定即可得出.
(2)记g(x)=kx2+4x+k+3,由g(x)≥0在R上有解,而k<0,由△≥0,得-4≤k<0,对k分类讨论,及其充要条件的判定即可得出.
解答:
解:(1)由(2+x)(3-x)≥0,化为(x+2)(x-3)≤0,解得-2≤x≤3.
∴A=[-2,3].
(2)记g(x)=kx2+4x+k+3,由g(x)≥0在R上有解,而k<0,
故△=16-4k(k+3)≥0,得-4≤k<0,①
当k=-4时,B={
},满足条件.
设g(x)=0的两个根x1,x2(x1<x2),则B=(x1,x2),
由x∈A是x∈B的必要不充分条件得:
,即
②
由①②得-4≤k≤-
.
∴A=[-2,3].
(2)记g(x)=kx2+4x+k+3,由g(x)≥0在R上有解,而k<0,
故△=16-4k(k+3)≥0,得-4≤k<0,①
当k=-4时,B={
| 1 |
| 2 |
设g(x)=0的两个根x1,x2(x1<x2),则B=(x1,x2),
由x∈A是x∈B的必要不充分条件得:
|
|
由①②得-4≤k≤-
| 3 |
| 2 |
点评:本题考查了一元二次不等式的解集与判别式的关系、分类讨论、充要条件的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
集合A={x|y=
},B={y|y=x2-1},则∁RA∪B=( )
| x2-4 |
| A、(-2,+∞) |
| B、[-2,+∞) |
| C、(-1,+∞) |
| D、[-1,+∞) |
已知偶函数f(x)在[0,+∞)单调递减,A(2,1)的其图象上.那么f(x+1)>1的解集为( )
| A、(-2,2) |
| B、(-3,1) |
| C、[0,2) |
| D、(-1,3) |
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
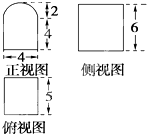

| A、92+24π |
| B、82+14π |
| C、92+14π |
| D、82+24π |
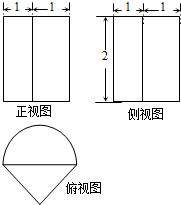 如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )
如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )A、2+3π+4
| ||
B、2+2π+4
| ||
C、8+5π+2
| ||
D、6+3π+2
|