题目内容
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,则cos∠DAC=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理的应用,三角形中的几何计算
专题:解三角形
分析:画出图形求出△ACD的三个边长,利用余弦定理求解即可.
解答:
 解:如图:直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,
解:如图:直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,
不妨令AB=2,则BC=CD=1,作ED⊥AB于E,可得AD=
,
AC=
=
.
在△ACD中,由余弦定理可得:
coscos∠DAC=
=
=
.
故选:B.
 解:如图:直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,
解:如图:直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,不妨令AB=2,则BC=CD=1,作ED⊥AB于E,可得AD=
| 2 |
AC=
| AB2+BC2 |
| 5 |
在△ACD中,由余弦定理可得:
coscos∠DAC=
| AD2+AC2-CD2 |
| 2AD•AC |
| 2+5-1 | ||||
2×
|
3
| ||
| 10 |
故选:B.
点评:本题考查三角形的解法,余弦定理的应用,画出图形是解题的关键.

练习册系列答案
相关题目
从高h米的小岛看正东方向有一只船俯角为30°,看正南方向有一只船俯角为45°,则此时两船间的距离为( )
| A、2h米 | ||
B、
| ||
C、
| ||
D、2
|
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}共有9项,其中a1=a9=1,且对每个i∈{1,2…,8},均有
∈{2,1,-
}|,记S=
+
+…+
,则S的最小值为( )
| ai+1 |
| ai |
| 1 |
| 2 |
| a2 |
| a1 |
| a3 |
| a2 |
| a9 |
| a8 |
| A、4 | B、6 | C、8 | D、10 |
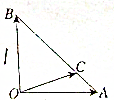 如图所示,在等腰Rt△AOB中,OA=OB=1,
如图所示,在等腰Rt△AOB中,OA=OB=1,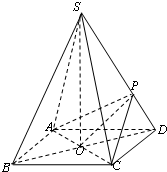 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的