题目内容
已知数列{an}共有9项,其中a1=a9=1,且对每个i∈{1,2…,8},均有
∈{2,1,-
}|,记S=
+
+…+
,则S的最小值为( )
| ai+1 |
| ai |
| 1 |
| 2 |
| a2 |
| a1 |
| a3 |
| a2 |
| a9 |
| a8 |
| A、4 | B、6 | C、8 | D、10 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:令bi=
,1≤i≤8),根据数列比值的关系,结合S的表达式进行推导即可.
| ai+1 |
| ai |
解答:
解:令bi=
(1≤i≤8),则对每个符合条件的数列{an},
满足
bi=
=
=1,且bi∈{2,1,-
},1≤i≤8.
反之,由符合上述条件的八项数列{bn}可唯一确定一个符合题设条件的九项数列{an}.
记符合条件的数列{bn}的个数为N,
由题意知bi(1≤i≤8)中有2k个-
,2k个2,8-4k个1,
且k的所有可能取值为0,1,2.
对于三种情况,当k=2时,S取到最小值6.
故选:B.
| ai+1 |
| ai |
满足
| 8 |
 |
| i=1 |
| 8 |
 |
| i=1 |
| ai+1 |
| ai |
| a9 |
| a1 |
| 1 |
| 2 |
反之,由符合上述条件的八项数列{bn}可唯一确定一个符合题设条件的九项数列{an}.
记符合条件的数列{bn}的个数为N,
由题意知bi(1≤i≤8)中有2k个-
| 1 |
| 2 |
且k的所有可能取值为0,1,2.
对于三种情况,当k=2时,S取到最小值6.
故选:B.
点评:本题考查数列的相邻两项比值之和的最小值的求法,考查满足条件的数列的个数的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,已知a1=2,S4=26.
(1)求数列{an}的通项公式;
(2)设Pn=a1+a4+…+a3n-2,Qn=a10+a12+…+a2n+8,试比较Pn与Qn的大小关系,并说明理由.
(1)求数列{an}的通项公式;
(2)设Pn=a1+a4+…+a3n-2,Qn=a10+a12+…+a2n+8,试比较Pn与Qn的大小关系,并说明理由.
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,则cos∠DAC=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,则f(0)=( )
|
| A、-1 | B、0 | C、1 | D、3 |
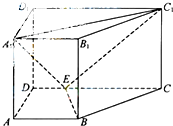 如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=