题目内容
17.设集合A={x|8+2x-x2>0},集合B={x|x=2n-1,n∈N*},则A∩B等于( )| A. | {-1,1} | B. | {-1,3} | C. | {1,3} | D. | {3,1,-1} |
分析 先分别求出集合A和B,再利用交集的定义求解.
解答 解:∵集合A={x|8+2x-x2>0}={x|-2<x<4},
集合B={x|x=2n-1,n∈N*}={正奇数},
∴A∩B={1,3}.
故选:C.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.设f′(x)是函数f(x)的导函数,且f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e(e为自然对数的底数),则不等式f(lnx)<x2的解集为( )
| A. | (0,$\frac{e}{2}$) | B. | (0,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | ($\frac{e}{2}$,$\sqrt{e}$) |
2.若p,q∈R,则|p|<|q|成立的一个充分不必要条件是( )
| A. | q>p>0 | B. | p>q>0 | C. | p<q<0 | D. | p=q≠0 |
7.设复数z满足(1+2i)z=5i,则复数z为( )
| A. | 2+i | B. | -2+i | C. | 2-i | D. | -2-i |
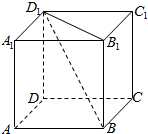 已知正方体ABCD-A1B1C1D1的棱长为a,
已知正方体ABCD-A1B1C1D1的棱长为a, 某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?
某食堂以面食和米食为主食,员工良好的日常饮食应该至少需要碳水化合物5个单位,蛋白质6个单位,脂肪6个单位,每份面食含有7个单位的碳水化合物,7个单位的蛋白质,14个单位的脂肪,花费28元;而每份米食含有7个单位的碳水化合物,14个单位的蛋白质,7个单位的脂肪,花费21元.为了满足员工的日常饮食要求,同时使花费最低,需要同时采购面食和米食各多少份?