题目内容
11.设f′(x)是函数f(x)的导函数,且f′(x)>2f(x)(x∈R),f($\frac{1}{2}$)=e(e为自然对数的底数),则不等式f(lnx)<x2的解集为( )| A. | (0,$\frac{e}{2}$) | B. | (0,$\sqrt{e}$) | C. | ($\frac{1}{e}$,$\frac{e}{2}$) | D. | ($\frac{e}{2}$,$\sqrt{e}$) |
分析 构造函数F(x)=$\frac{f(x)}{{e}^{2x}}$,求出导数,判断F(x)在R上递增.原不等式等价为F(lnx)<F($\frac{1}{2}$),运用单调性,可得lnx<$\frac{1}{2}$,运用对数不等式的解法,即可得到所求解集.
解答 解:可构造函数F(x)=$\frac{f(x)}{{e}^{2x}}$,
F′(x)=$\frac{f(x){e}^{2x}-2f(x){e}^{2x}}{({e}^{2x})^{2}}$=$\frac{f′(x)-2f(x)}{{e}^{2x}}$,
由f′(x)>2f(x),可得F′(x)>0,即有F(x)在R上递增.
不等式f(lnx)<x2即为$\frac{f(lnx)}{{x}^{2}}$<1,(x>0),即$\frac{f(lnx)}{{e}^{2lnx}}$<1,x>0.
即有F($\frac{1}{2}$)=$\frac{f(\frac{1}{2})}{e}$=1,即为F(lnx)<F($\frac{1}{2}$),
由F(x)在R上递增,可得lnx<$\frac{1}{2}$,解得0<x<$\sqrt{e}$.
故不等式的解集为(0,$\sqrt{e}$),
故选:B.
点评 本题考查导数的运用:求单调性,考查构造法的运用,以及单调性的运用,对数不等式的解法,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
2.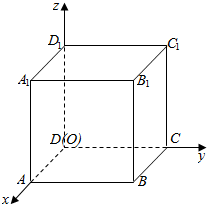 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )| A. | (1,$\sqrt{2}$,$\sqrt{2}$) | B. | (1,1,$\sqrt{2}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}$,1) |
6.“-$\sqrt{2}$≤k≤$\sqrt{2}$”是“直线x-y+k=0与圆x2+y2=1相交”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
17.设集合A={x|8+2x-x2>0},集合B={x|x=2n-1,n∈N*},则A∩B等于( )
| A. | {-1,1} | B. | {-1,3} | C. | {1,3} | D. | {3,1,-1} |
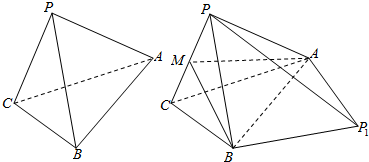 如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.
如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.