题目内容
6.设m、n是两条不同的直线,α、β、γ是三个不同的平面,给出下列四个命题,其中正确命题的序号是( )①若m⊥α,n⊥α,则m⊥n;
②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,n∥α,则m∥n;
④若α⊥γ,β⊥γ,则α⊥β.
| A. | ② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 ①利用线面垂直的性质可得:若m⊥α,n⊥α,则m∥n;
②利用平面平行的传递性和平行平面的性质可得:若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ;
③利用线面平行的性质可得:若m∥α,n∥α,则m∥n、相交或为异面直线;
④利用面面垂直的性质可得:若α⊥γ,β⊥γ,则α∥β或相交.
解答 解:①若m⊥α,n⊥α,则m∥n,因此①不正确;
②若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ,正确;
③若m∥α,n∥α,则m∥n、相交或为异面直线,因此不正确;
④若α⊥γ,β⊥γ,则α∥β或相交,因此不正确.
综上可知:只有②正确.
点评 本题综合考查了空间中线面的位置关系及其判定性质,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
16.已知集合P={x|1<3x≤9},Q={x∈Z|y=ln(-2x2+7x)},则P∩Q=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
1.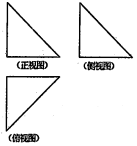 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
18.已知△ABC中,C=90°,AB=2AC,在斜边AB上任取一点P,则满足∠ACP≤30°的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
15.已知向量$\overrightarrow{a}$=(2,-1,3),$\overrightarrow{b}$=(-4,2,x),使$\overrightarrow{a}$∥$\overrightarrow{b}$成立的x为( )
| A. | -6 | B. | 6 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
16.已知集合M={5,log2a},N={a,b},若M∩N={1},则M∪N=( )
| A. | {1,2,5} | B. | {0,1,2} | C. | {0,1,5} | D. | {0,2,5} |