题目内容
16.若实数x,y满足x2+y2≤4,求以下代数式的最值.(1)$\frac{y-2}{x+3}$,(2)|3x-2y+1|;(3)x2+2x+y2-y+1.
分析 (1)$\frac{y-2}{x+3}$表示圆上的点M(x,y)与点A(-3,2)连线的斜率,当直线MA和圆相切时,由圆心(0,0)到直线的距离等于半径2,求得k的值,可得$\frac{y-2}{x+3}$的范围.
(2)令 t=|3x-2y+1|,故当直线3x-2y+1±t=0和圆x2+y2=4相切时,t取得最值,由得$\frac{|0-0+1±t|}{\sqrt{9+4}}$=2,求得t的值,即为所求.
(3)x2+2x+y2-y+1=(x+1)2+${(y-\frac{1}{2})}^{2}$-$\frac{1}{4}$,表示圆内的点(含边界)与点N(-1,$\frac{1}{2}$)之间的距离的平方减去$\frac{1}{4}$,求得NO,可得x2+2x+y2-y+1的最大值和最小值.
解答 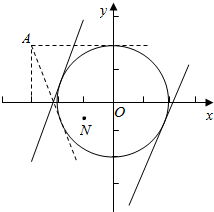 解:由于实数x,y满足x2+y2≤4,则点(x,y)位于以原点为圆心、以2为半径的圆的内部(包含圆),
解:由于实数x,y满足x2+y2≤4,则点(x,y)位于以原点为圆心、以2为半径的圆的内部(包含圆),
(1)$\frac{y-2}{x+3}$表示圆上的点M(x,y)与点A(-3,2)连线的斜率 k,
当直线MA和圆相切时,由圆心(0,0)到直线y-2=k(x+3)的距离等于半径2,
可得$\frac{|0-0+3k+2|}{\sqrt{{k}^{2}+1}}$=2,求得k=0,或 k=-$\frac{12}{5}$,
故$\frac{y-2}{x+3}$∈[-$\frac{12}{5}$,0].
(2)令 t=|3x-2y+1|,则3x-2y+1=±t,故当直线3x-2y+1±t=0和圆x2+y2=4相切时,
t取得最值.
根据圆心(0,0)到直线3x-2y+1±t=0 的距离等于半径2,可得$\frac{|0-0+1±t|}{\sqrt{9+4}}$=2,
即|t-1|=2$\sqrt{13}$,求得t=2$\sqrt{13}$+1,或 t=2$\sqrt{13}$-1,故t的最大值为2$\sqrt{13}$+1,最小值为2$\sqrt{13}$-1.
(3)x2+2x+y2-y+1=(x+1)2+${(y-\frac{1}{2})}^{2}$-$\frac{1}{4}$,表示圆内的点(含边界)与点N(-1,$\frac{1}{2}$)之间的距离的平方减去$\frac{1}{4}$,
求得NO2=$\frac{5}{4}$,故x2+2x+y2-y+1的最大值为${(2+\frac{\sqrt{5}}{2})}^{2}$-$\frac{1}{4}$=5+2$\sqrt{5}$;x2+2x+y2-y+1的最小值为0-$\frac{1}{4}$=-$\frac{1}{4}$.
点评 本题主要考查圆的标准方程,直线的斜率公式、两点间的距离公式,体现了数形结合的数学思想,属于中档题.

| A. | f(x)=x | B. | f(x)=sinx | C. | f(x)=x2 | D. | f(x)=x+1 |
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
| A. | 2 | B. | 1 | C. | ±2 | D. | $\frac{1}{2}$ |