题目内容

6．已知椭圆两焦点为F1，F2，a=$\frac{3}{2}$，过F1作直线交椭圆于A，B两点，求△ABF2的周长．

分析 由椭圆的定义可得，|AF1|+|AF2|=2a，|BF1|+|BF2|=2a，即可得到所求周长为4a，代入数据即可得到所求．

解答 解：由椭圆的定义可得，|AF1|+|AF2|=2a，
|BF1|+|BF2|=2a，
可得△ABF2的周长为|AF2|+|BF2|+|AB|=（|AF1|+|AF2|）+（|BF1|+|BF2|）
=2a+2a=4a=4×$\frac{3}{2}$=6．
则△ABF2的周长为6．

点评 本题考查椭圆的定义的运用，考查三角形的周长的求法，注意圆锥曲线中的定义法的运用，属于基础题．

练习册系列答案
相关题目
16．直线l过抛物线y2=2px（p＞0）的焦点，且交抛物线于A，B两点，交其准线于C点，已知|AF|=3，$\overrightarrow{CB}$=3$\overrightarrow{BF}$，则p=2．
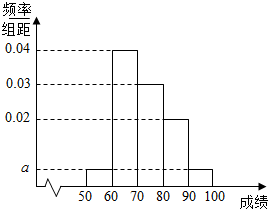17．某校高二年级有1200人，从中抽取100名学生，对其期中考试语文成绩进行统计分析，得到如图所示的频率分布直方图，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100]．
（Ⅰ）求图中a的值并估计语文成绩的众数；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（Ⅲ） 根据频率分布直方图，估计该校这1200名学生中成绩在60分（含60分）以上的人数．
14．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，作$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{a}$+$\overrightarrow{b}$，则∠AOB=30°．（用角度表示）
1．“鸡兔同笼”是我国隋朝时期的数学著作《孙子算经》中的一个有趣而具有深远影响的题目：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”请画出一个解决这个问题的程序框图．
11．函数y=tan2x-2tanx，x$∈[0，\frac{π}{2}）$的最小值是-1．
18．从0，1，…，9中选出三个不同数字组成四位数（其中的一个数字可以出现两次），如5224．则这样的四位数共有3888个．
15．已知f（x）=-$\frac{\sqrt{2}}{2}$sin（2x+$\frac{π}{4}$）+2，求：
（1）f（x）的最小正周期及对称轴方程；
（2）f（x）的单调递增区间；
（3）若方程f（x）-m+1=0在x∈[0，$\frac{π}{2}$]上有解，求实数m的取值范围．
16．若实数x，y满足x2+y2≤4，求以下代数式的最值．
（1）$\frac{y-2}{x+3}$，（2）|3x-2y+1|；（3）x2+2x+y2-y+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网