题目内容

7．函数y=cos2x+$\sqrt{3}$sinx+1（x∈R）的最大值为$\frac{11}{4}$，最小值为1-$\sqrt{3}$．

分析 由条件正弦函数的值域，二次函数的性质，求得函数y的最值．

解答 解：函数y=cos2x+$\sqrt{3}$sinx+1=-sin2x+$\sqrt{3}$sinx+2=-${（sinx-\frac{\sqrt{3}}{2}）}^{2}$+$\frac{11}{4}$，
故当sinx=$\frac{\sqrt{3}}{2}$时，函数y取得最大值为 $\frac{11}{4}$，当sinx=-1时，函数y取得最小值为1-$\sqrt{3}$，
故答案为：$\frac{11}{4}$；1-$\sqrt{3}$．

点评 本题主要考查正弦函数的值域，二次函数的性质，属于基础题．

练习册系列答案
相关题目
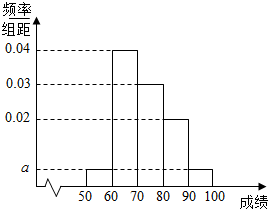17．某校高二年级有1200人，从中抽取100名学生，对其期中考试语文成绩进行统计分析，得到如图所示的频率分布直方图，其中成绩分组区间是：[50，60）、[60，70）、[70，80）、[80，90）、[90，100]．
（Ⅰ）求图中a的值并估计语文成绩的众数；
（Ⅱ）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（Ⅲ） 根据频率分布直方图，估计该校这1200名学生中成绩在60分（含60分）以上的人数．
18．从0，1，…，9中选出三个不同数字组成四位数（其中的一个数字可以出现两次），如5224．则这样的四位数共有3888个．
15．已知f（x）=-$\frac{\sqrt{2}}{2}$sin（2x+$\frac{π}{4}$）+2，求：
（1）f（x）的最小正周期及对称轴方程；
（2）f（x）的单调递增区间；
（3）若方程f（x）-m+1=0在x∈[0，$\frac{π}{2}$]上有解，求实数m的取值范围．
2．已知定义在R上奇函数f（x）满足f（x+2）=-f（x），且x∈（0，1]时，f（x）=2x，求值：
（1）f（98）=0；
（2）f（$\frac{17}{2}$）=$\sqrt{2}$；
（3）f（$\frac{100}{3}$）=$\root{3}{4}$；
（4）f（log218）=$\frac{9}{4}$；
（5）f（2015）=-2．
12．已知函数f（x）=$\left\{\begin{array}{l}{8，（x=1）}\\{f（x-1）+3，（x≥2，x∈{N}^{*}）}\end{array}\right.$，求f（3）．
19．化简：$\frac{1}{co{s}^{2}α\sqrt{1+ta{n}^{2}α}}$-$\sqrt{\frac{1+sinα}{1-sinα}}$（α为第二象限角）
16．若实数x，y满足x2+y2≤4，求以下代数式的最值．
（1）$\frac{y-2}{x+3}$，（2）|3x-2y+1|；（3）x2+2x+y2-y+1．
5．已知函数f（x）=ln（ax）（a≠0，a∈R），g（x）=$\frac{x-1}{x}$．
（Ⅰ）当a=1时，记φ（x）=f（x）-$\frac{x+1}{x-1}$，求函数φ（x）的单调区间；
（Ⅱ）若f（x）≥g（x）（x≥1）恒成立，求实数a的取值范围；
（Ⅲ） 已知对于0＜λ＜1，恒有$\frac{{1+{k^λ}}}{2}≤{（\frac{1+k}{2}）^λ}$（k∈N*）成立；当a=1且0＜λ＜1时，对任意n∈N*，试比较$\sum_{k=1}^n{\frac{1}{{1+{k^λ}}}}$与f[（1+n）λ2n（1-λ）]的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网