题目内容
20．设集合M={x|y=ln（x-1）}，N={x|x=2t，-1≤t≤2}，则M∩N=（ ）| A． | （1，4] | B． | [$\frac{1}{2}$，1） | C． | （1，2] | D． | [2，4] |
分析 求出集合的等价条件，根据集合的基本运算进行求解即可．
解答 解：M={x|y=ln（x-1）}={x|x-1＞0}={x|x＞1}，N={x|x=2t，-1≤t≤2}={x|$\frac{1}{2}$≤x≤4}，
则M∩N={x|1＜x≤4}=（1，4]，
故选：A
点评 本题主要考查集合的基本运算，根据函数的性质求出集合的等价条件是解决本题的关键．
练习册系列答案
53随堂测系列答案
相关题目
10．已知向量$|{\overrightarrow a}|=2，|{\overrightarrow b}|=1，|{\overrightarrow a-2\overrightarrow b}|=2\sqrt{3}$，则向量$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | 30o | B． | 60o | C． | 120o | D． | 150o |
15．从已有3个红球、2个白球的袋中任取3个球，设A={至少取到两个红球}，B={恰好取到一个白球}，则事件AB的概率是（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{9}{10}$ |
12．下列说法错误的是（ ）
| A． | 命题“若x2-4x+3=0，则x=3或x=1”的逆否命题是“若x≠3且x≠1，则x2-4x+3=0≠0” | |
| B． | “x2-x=0”是“x=1”的必要不充分条件 | |
| C． | 若p∨q为真命题，则p，q均为真命题 | |
| D． | 命题p：?x∈R，使得x3+x+1=0，则￢p：?x∈R，使得x3+x+1≠0 |
函数y=2sinπx（x∈R）的部分图象如图所示，设O为坐标原点，P是图象的最高点，B是图象与x轴的交点，则tan∠OPB的值为$\frac{16}{3}$．
10．
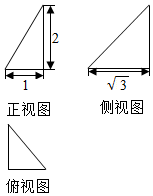某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）| A． | $\frac{25π}{4}$ | B． | $\frac{25π}{8}$ | C． | 12π | D． | 8π |