题目内容
9. 函数y=2sinπx(x∈R)的部分图象如图所示,设O为坐标原点,P是图象的最高点,B是图象与x轴的交点,则tan∠OPB的值为$\frac{16}{3}$.
函数y=2sinπx(x∈R)的部分图象如图所示,设O为坐标原点,P是图象的最高点,B是图象与x轴的交点,则tan∠OPB的值为$\frac{16}{3}$.
分析 过P作PQ垂直于x轴,根据正弦函数的图象与性质,得出点P、B和Q的坐标,计算|PQ|,|OQ|,|BQ|的长,
利用锐角三角函数定义表示出tan∠OPQ和tan∠BPQ,计算tan∠OPB的值即可.
解答 解:过P作PQ⊥x轴,如图所示: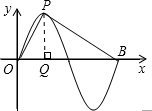
∵函数y=2sinπx,且P是图象的最高点,B是图象与x轴的交点,
∴P($\frac{1}{2}$,2),B(2,0),
即|PQ|=2,|OQ|=$\frac{1}{2}$,|OB|=2,
∴|QB|=|OB|-|OQ|=$\frac{3}{2}$,
在Rt△OPQ中,tan∠OPQ=$\frac{|OQ|}{|PQ|}$=$\frac{1}{4}$,
在Rt△PQB中,tan∠BPQ=$\frac{|BQ|}{|PQ|}$=$\frac{3}{4}$,
∴tan∠OPB=tan(∠OPQ+∠BPQ)=$\frac{\frac{1}{4}+\frac{3}{4}}{1-\frac{1}{4}×\frac{3}{4}}$=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查了两角和与差的正切函数公式,锐角三角函数定义以及正弦函数的图象与性质,作出辅助线PQ,找P、B的坐标是解题的关键.

练习册系列答案
相关题目
20.设集合M={x|y=ln(x-1)},N={x|x=2t,-1≤t≤2},则M∩N=( )
| A. | (1,4] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2,4] |
14. 如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
 如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )
如图,函数y=log24x图象上的两点A,B和y=log2x上的点C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则p2×2q=( )| A. | 12 | B. | $12\sqrt{3}$ | C. | 6 | D. | $6\sqrt{3}$ |
18.如图所示的算法流程图中,第3个输出的数是( )


| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
1.在两个学习基础相当的班级实行某种教学措施的实验,测试结果见表,则实验效果与教学措施( )
| 优、良、中 | 差 | 总计 | |
| 实验班 | 48 | 2 | 50 |
| 对比班 | 38 | 12 | 50 |
| 总计 | 86 | 14 | 100 |
| A. | 有关 | B. | 无关 | C. | 关系不明确 | D. | 以上都不正确 |
 如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2
如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2