题目内容
10.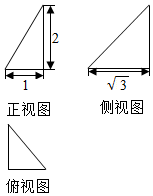 某几何体的三视图如图所示,则该几何体外接球的表面积为( )
某几何体的三视图如图所示,则该几何体外接球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{25π}{8}$ | C. | 12π | D. | 8π |
分析 由几何体的三视图知该几何体是三棱锥S-ABC,底面△ABC中,AC=1,AB=$\sqrt{3}$,∠CAB=90°,AS⊥平面ABC,且SA=2,该几何体外接球半径是以AC,AB,AS为棱长的长方体的体对角线长的一半,由此能求出该几何体外接球的表面积.
解答  解:由几何体的三视图知该几何体是如图所示的三棱锥S-ABC,
解:由几何体的三视图知该几何体是如图所示的三棱锥S-ABC,
其中底面△ABC中,AC=1,AB=$\sqrt{3}$,∠CAB=90°,AS⊥平面ABC,且SA=2,
∴该几何体外接球半径是以AC,AB,AS为棱长的长方体的体对角线长的一半,
∴该几何体外接球半径R=$\frac{\sqrt{A{C}^{2}+A{B}^{2}+A{S}^{2}}}{2}$=$\frac{\sqrt{1+3+4}}{2}$=$\sqrt{2}$,
∴该几何体外接球的表面积为S=4πR2=4π•2=8π.
故选:D.
点评 本题考查几何体外接球的表面积的求法,是基础题,解题时要认真审题,注意三视图的性质的合理运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
20.设集合M={x|y=ln(x-1)},N={x|x=2t,-1≤t≤2},则M∩N=( )
| A. | (1,4] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2,4] |
18.如图所示的算法流程图中,第3个输出的数是( )


| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
1.在两个学习基础相当的班级实行某种教学措施的实验,测试结果见表,则实验效果与教学措施( )
| 优、良、中 | 差 | 总计 | |
| 实验班 | 48 | 2 | 50 |
| 对比班 | 38 | 12 | 50 |
| 总计 | 86 | 14 | 100 |
| A. | 有关 | B. | 无关 | C. | 关系不明确 | D. | 以上都不正确 |
2.已知函数$f(x)=\left\{{\begin{array}{l}{{x^2},(x≤0)}\\{\sqrt{4-{x^2}}(x>0)}\end{array}}\right.$,则$\int_{-1}^2{f(x)dx}$=( )
| A. | $π-\frac{1}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{π}{4}+\frac{1}{3}$ | D. | $\frac{π}{2}-\frac{1}{3}$ |
 如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
如图所示,已知⊙O的半径是1,点C在直径AB的延长线上,BC=1,点P是⊙O上半圆上的一个动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.