题目内容
8.已知lg2=a,lg3=b,则lg$\frac{3}{2}$=b-a.分析 利用对数的运算法则即可得出.
解答 解:lg$\frac{3}{2}$=lg3-lg2=b-a.
故答案为:b-a.
点评 本题考查了对数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
18.已知f(x)=x2+px+q和$g(x)=x+\frac{4}{x}$是定义在$A=\left\{{x|1≤x≤\frac{5}{2}}\right\}$上的函数,对任意的x∈A,存在常数x0∈A,使f(x)≥f(x0),g(x)≥g(x0)且f(x0)=g(x0),则f(x)在A上的最大值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{17}{4}$ | C. | 5 | D. | $\frac{41}{10}$ |
16.已知点A(1,-3),B(-5,5),则线段AB中点到直线4x-3y+1=0的距离等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{10}{7}$ | C. | $\frac{12}{5}$ | D. | 2 |
3.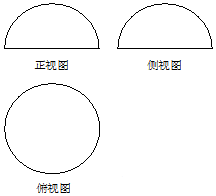 如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
 如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )
如图是一个几何体的三视图,正视图、侧视图是半径为R的半圆,俯视图是半径为R的圆,若该几何体的表面积为6π,则R=( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
20.设集合M={x|y=ln(x-1)},N={x|x=2t,-1≤t≤2},则M∩N=( )
| A. | (1,4] | B. | [$\frac{1}{2}$,1) | C. | (1,2] | D. | [2,4] |
18.如图所示的算法流程图中,第3个输出的数是( )


| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
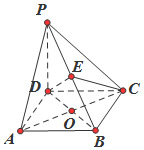 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点. 如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2
如图所示,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB=2