题目内容
求下列函数的值域:
(1)y=
;
(2)y=
.
(1)y=
| 1-2x |
| 1+3x |
(2)y=
1-2
| ||
1+3
|
考点:函数的值域
专题:函数的性质及应用
分析:(1)变形可得x=
,由分母不为0可得y的范围,可得值域;
(2)同(1)可得
=
,由
≥0可得
≥0,解关于y的不等式可得所求.
| 1-y |
| 3y+2 |
(2)同(1)可得
| x |
| 1-y |
| 3y+2 |
| x |
| 1-y |
| 3y+2 |
解答:
解:(1)∵y=
,∴y(1+3x)=1-2x,
变形可得x=
,可得3y+2≠0,
解得y≠-
,故函数的值域为:{y|y≠-
};
(2)∵y=
,同(1)可得
=
,
∵
≥0,∴
≥0,
解不等式可得-
≤y≤1,
故函数的值域为:{y|-
≤y≤1}
| 1-2x |
| 1+3x |
变形可得x=
| 1-y |
| 3y+2 |
解得y≠-
| 2 |
| 3 |
| 2 |
| 3 |
(2)∵y=
1-2
| ||
1+3
|
| x |
| 1-y |
| 3y+2 |
∵
| x |
| 1-y |
| 3y+2 |
解不等式可得-
| 2 |
| 3 |
故函数的值域为:{y|-
| 2 |
| 3 |
点评:本题考查函数值域的求解,反函数法是解决问题的关键,属基础题.

练习册系列答案
相关题目
“m=1”是“复数z=(1+mi)(1+i)(m∈R,i为虚数单位)为纯虚数”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
在正方体ABCD-A1B1C1D1中,M,N分别C1D1,BC是的中点,则下列判断正确的是( )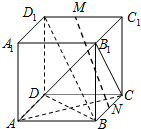

| A、MN∥BD1 |
| B、MN⊥AB1 |
| C、MN∥平面BDD1 |
| D、MN⊥平面AB1C |