题目内容
已知抛物线y2=2px(p>0)的焦点为双曲线
-
=1(a>0,b>0)的一个焦点,且两条曲线都经过点M(2,4).
(1)求这两条曲线的标准方程;
(2)已知点P在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点P的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求这两条曲线的标准方程;
(2)已知点P在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用抛物线y2=2px(p>0)经过点M(2,4),可得抛物线方程,利用双曲线的定义或待定系数法,可求双曲线的标准方程;
(2)设点P的坐标为(xp,yp),由题意得,S△PF1F2=
F 1F2•|yP|=2•|yP|=4,即可求点P的坐标.
(2)设点P的坐标为(xp,yp),由题意得,S△PF1F2=
| 1 |
| 2 |
解答:
解:(1)∵抛物线y2=2px(p>0)经过点M(2,4),
∴42=2p×2,解得p=4,
∴抛物线的标准方程为y2=8x.…(3分)
∴抛物线的焦点为(2,0),
∴双曲线的焦点为F1(-2,0),F2(2,0).
法一:∴MF1=
=4
,MF2=
=4,
∴2a=|MF1-MF2|=4
-4,a=2
-2,a2=12-8
. …(5分)
∴b2=c2-a2=4-(12-8
)=8
-8.
∴双曲线的标准方程为
-
=1.…(8分)
法二:a2+b2=c2=4,∵双曲线经过点M(2,4),∴
-
=1,…(5分)
解得 a2=12-8
,b2=8
-8.
∴双曲线的标准方程为
-
=1.…(8分)
(2)设点P的坐标为(xp,yp),
由题意得,S△PF1F2=
F 1F2•|yP|=2•|yP|=4,
∴yP=±2,…(11分)
∵点P在抛物线上,∴xP=
,
∴点P的坐标为(
,2)或(
,-2).…(14分)
∴42=2p×2,解得p=4,
∴抛物线的标准方程为y2=8x.…(3分)
∴抛物线的焦点为(2,0),
∴双曲线的焦点为F1(-2,0),F2(2,0).
法一:∴MF1=
| (2+2)2+42 |
| 2 |
| (2-2)2+42 |
∴2a=|MF1-MF2|=4
| 2 |
| 2 |
| 2 |
∴b2=c2-a2=4-(12-8
| 2 |
| 2 |
∴双曲线的标准方程为
| x2 | ||
12-8
|
| y2 | ||
8
|
法二:a2+b2=c2=4,∵双曲线经过点M(2,4),∴
| 4 |
| a2 |
| 16 |
| b2 |
解得 a2=12-8
| 2 |
| 2 |
∴双曲线的标准方程为
| x2 | ||
12-8
|
| y2 | ||
8
|
(2)设点P的坐标为(xp,yp),
由题意得,S△PF1F2=
| 1 |
| 2 |
∴yP=±2,…(11分)
∵点P在抛物线上,∴xP=
| 1 |
| 2 |
∴点P的坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查椭圆方程,双曲线方程,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合M={x||x|>2},N={x|x>1},则M∩N=( )
| A、{x|x<-2或x>2} |
| B、{x|x>2} |
| C、{x|x>1} |
| D、{x|x<1} |
下列说法中,正确的是( )
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 |
| B、已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
| C、命题“p∨q”为真命题,则“命题p”和“命题q”均为真命题 |
| D、已知x∈R,则“x2-2x-3=0”是“x=3”的必要不充分条件 |
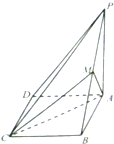 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=