题目内容
已知等差数列{an}的公差d≠0,a1=2,且a4,a6,a9成等比数列.
(1)求通项公式an;
(2)令bn=an+1+2n,n∈N*,求数列{bn}的前n项的和Tn.
(1)求通项公式an;
(2)令bn=an+1+2n,n∈N*,求数列{bn}的前n项的和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)首先利用已知条件求出等差数列的首项和公差,进一步求出数列的通项公式.
(2)根据(1)的结论,利用分类的方法求数列的和.
(2)根据(1)的结论,利用分类的方法求数列的和.
解答:
解:(1)a62=a4•a9⇒(a1+5d)2=(a1+3d)•(a1+8d),
d2=a1d,
因为d≠0,
则d=a1=2.
所以an=2+(n-1)•2=2n
(2)因为bn=2n+1+2n,
所以Tn=2(1+2+3+…+n)+n+(21+22+…+2n)
=
+n+
=n2+2n+2n+1-2
d2=a1d,
因为d≠0,
则d=a1=2.
所以an=2+(n-1)•2=2n
(2)因为bn=2n+1+2n,
所以Tn=2(1+2+3+…+n)+n+(21+22+…+2n)
=
| 2n(n+1) |
| 2 |
| 2(1-2n) |
| 1-2 |
=n2+2n+2n+1-2
点评:本题考查的知识要点:数列通项公式的求法,利用分类求和的方法求数列的和.属于基础题型.

练习册系列答案
相关题目
将函数y=3sin(2x-
)的图象经过( )变换,可以得到函数y=3sin2x的图象.
| π |
| 4 |
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向右平移
| ||
D、沿x轴向左平移
|
圆(x-2)2+y2=4过点P(1,
)的切线方程是( )
| 3 |
A、x+
| ||
B、x+
| ||
C、x-
| ||
D、x-
|
若a<b<0,则下列不等式成立的是( )
| A、ac<bc<0 | ||||
B、
| ||||
C、
| ||||
| D、a2>b2 |
下表中与数x对应的lgx值有且只有一个是错误的,则错误的是( )
| x | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| lgx | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
| A、lg6=1+a-b-c |
| B、lg8=3-3a-3c |
| C、lg12=3-b-2c |
| D、lg27=6a-3b |
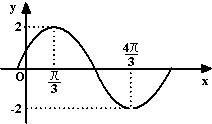 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<