题目内容
15.欧位在1748年给出的著名公式eiθ=cosθ+isinθ(欧拉公式)是数学中最卓越的公式之一,其中,底数e=2.71828…,根据欧拉公式eiθ=cosθ-isinθ.任何一个复数z=r(cosθ+isinθ)都呆以表示成z=reiz的形式,我们把这种形式叫做复数的指数形式,若复数z1=2ei${\;}^{\frac{π}{3}}$,z2=ei${\;}^{\frac{π}{2}}$,则复数z=$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 复数z1=2ei${\;}^{\frac{π}{3}}$=2$(cos\frac{π}{3}+isin\frac{π}{3})$=1+$\sqrt{3}$i,z2=ei${\;}^{\frac{π}{2}}$=$cos\frac{π}{2}+isin\frac{π}{2}$=i,再利用复数的运算法则、几何意义即可得出.
解答 解:复数z1=2ei${\;}^{\frac{π}{3}}$=2$(cos\frac{π}{3}+isin\frac{π}{3})$=1+$\sqrt{3}$i,z2=ei${\;}^{\frac{π}{2}}$=$cos\frac{π}{2}+isin\frac{π}{2}$=i,
则复数z=$\frac{{z}_{1}}{{z}_{2}}$=$\frac{1+\sqrt{3}i}{i}$=$\frac{-i(1+\sqrt{3}i)}{-ii}$=$\sqrt{3}$-i在复平面内对应的点$(\sqrt{3},-1)$在第四象限.
故选:D.
点评 本题考查了复数的指数与三角函数形式、复数的运算法则几何意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
15.将函数f(x)=sinωx(ω>0)的图象向右平移$\frac{π}{4}$个单位长度,所得图象关于点$({\frac{3π}{4},0})$对称,则ω的最小值是( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | 2 |
3.若直线l1:x+ay+6=0与l2:(a-2)x+3y+2a=0平行,则l1与l2间的距离为( )
| A. | $\sqrt{2}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
10.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )
| A. | 24里 | B. | 48里 | C. | 96里 | D. | 192里 |
20.设i是虚数但单位,则复数$z=\frac{2i+3}{1-i}$的共轭复数的虚部为( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{2}$ |
7.如图的框图是一古代数学家的一个算法的程序框图,它输出的结果S表示( )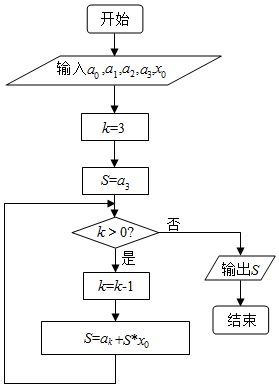

| A. | a0+a1+a2+a3的值 | B. | a3+a2x0+a1x02+a0x03的值 | ||
| C. | a0+a1x0+a2x02+a3x03的值 | D. | 以上都不对 |
4.已知{an}是等差数列,a10=17,其前10项的和S10=80,则其公差d=( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |