题目内容
5．已知（x2+2x+3y）5的展开式中x5y2（ ）| A． | 60 | B． | 180 | C． | 520 | D． | 540 |
分析 利用分步相乘原理，可以得出x5y2的系数．
解答 解：（x2+2x+3y）5可看作5个（x2+2x+3y）相乘，
从中选2个y，有C52种选法；
再从剩余的三个括号里边选出2个x2，最后一个括号选出x，有C32•C11种选法；
∴x5y2的系数为32C52•C32•2•C11=540，
故选：D
点评 本题考查了二项式定理的灵活应用问题，也考查了分步相乘原理的应用问题，是基础题目．
练习册系列答案
相关题目
14．
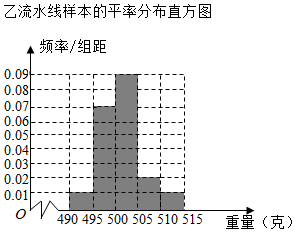某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本，并称出它们的重量（单位：克），重量值落在[495，510）内的产品为合格品，否则为不合格品，统计结果如表：
甲流水线样本的频数分布表
（1）求甲流水线样本合格的频率；
（2）从乙流水线上重量值落在[505，515]内的产品中任取2个产品，求这2件产品中恰好只有一件合格的概率．
某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本，并称出它们的重量（单位：克），重量值落在[495，510）内的产品为合格品，否则为不合格品，统计结果如表：甲流水线样本的频数分布表
| 产品重量（克） | 频数 |
| [490，495） | 6 |
| [495，500） | 8 |
| [500，505） | 14 |
| [505，510） | 8 |
| [510，515] | 4 |
（2）从乙流水线上重量值落在[505，515]内的产品中任取2个产品，求这2件产品中恰好只有一件合格的概率．
13．已知全集U={1，2，3，4，5，6}，M={2，3，4}，N={4，5}，则∁U（M∪N）=（ ）
| A． | {1，3，5} | B． | {2，4，6} | C． | {1，5} | D． | {1，6} |
20．已知球的直径SC=4，A、B 是该球面上的两点且AB=2$\sqrt{2}$，∠ASC=30°，∠SCB=45°，则三棱锥S-ABC的体积为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{2}$ | C． | $\frac{2}{3}\sqrt{3}$ | D． | $\frac{4}{3}\sqrt{3}$ |
17．下列哪个命题的逆命题为真命题的是（ ）
| A． | 若a＞b，则ac＞bc | B． | 若a2＞b2，则a＞b＞0 | ||
| C． | 若|x-3|＞1，则2＜x＜4 | D． | 若|x2-3|＞1，则$\sqrt{2}＜x＜2$ |
14．已知数列{an}的前n项和Sn=an2+bn（a，b∈R）且a2=3，a6=11，则S7等于（ ）
| A． | 13 | B． | 35 | C． | 49 | D． | 63 |
15．已知抛物线x2=2y的焦点与椭圆$\frac{{y}^{2}}{m}$+$\frac{{x}^{2}}{2}$=1的一个焦点重合，则m=（ ）
| A． | $\frac{9}{4}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{3}{2}$ |