题目内容
17.下列哪个命题的逆命题为真命题的是( )| A. | 若a>b,则ac>bc | B. | 若a2>b2,则a>b>0 | ||
| C. | 若|x-3|>1,则2<x<4 | D. | 若|x2-3|>1,则$\sqrt{2}<x<2$ |
分析 根据逆命题的定义,给出四个命题的逆命题,并判断真假,即可得到答案.
解答 解:若a>b,则ac>bc的逆命题为:若ac>bc,则a>b,在c≤0时不成立,故A不满足条件;
若a2>b2,则a>b>0的逆命题为:若a>b>0,则a2>b2,为真命题,故B满足条件;
若|x-3|>1,则2<x<4的逆命题为:若2<x<4,则|x-3|>1,为假命题,故C不满足条件;
若|x2-3|>1,则$\sqrt{2}<x<2$的逆命题为:若$\sqrt{2}<x<2$,则|x2-3|>1,为假命题,故D不满足条件;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了四种命题,不等式与不等关系,难度中档.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
5.已知(x2+2x+3y)5的展开式中x5y2( )
| A. | 60 | B. | 180 | C. | 520 | D. | 540 |
12.已知平面直角坐标系xoy,以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}\right.(φ为参数)$.点A,B是曲线C上两点,点A,B的极坐标分别为$({ρ_1},\frac{π}{3}),({ρ_2},\frac{5π}{6})$.则|AB|=( )
| A. | 4 | B. | $\sqrt{7}$ | C. | $4\sqrt{7}$ | D. | 5 |
9.方程$\sqrt{{{({x-3})}^2}+{y^2}}-\sqrt{{{({x+3})}^2}+{y^2}}=4$化简的结果是( )
| A. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$(x≤-2) | D. | $\frac{y^2}{5}-\frac{x^2}{4}=1$(y$≤-\sqrt{5}$) |
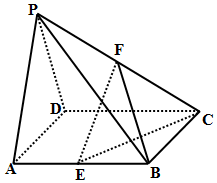 如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.