题目内容
20.已知球的直径SC=4,A、B 是该球面上的两点且AB=2$\sqrt{2}$,∠ASC=30°,∠SCB=45°,则三棱锥S-ABC的体积为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2}{3}\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
分析 设球心为O,连结AO、BO,取CO的中点D,连结AD.由球的直径的性质可得△SAC中,∠SAC=90°,结合∠ASC=30°且SC=4,算出AC=2,可得△AOC是边长为2的正三角形,得出AD⊥SC且AD=$\sqrt{3}$,再由已知可得△SBC是等腰直角三角形,求得BC,BS,结合已知可得BO⊥平面SAC,再利用锥体的体积公式加以计算,可得三棱锥S-ABC的体积.
解答 解: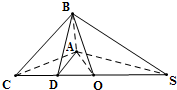 设球心为O,连结AO、BO,取CO的中点D,连结AD,
设球心为O,连结AO、BO,取CO的中点D,连结AD,
∵SC为球的直径,A、B是球面上的点,∴∠SAC=∠SBC=90°.
又∵∠ASC=30°,∠SCB=45°,SC=4,∴AC=2,BC=$2\sqrt{2}$.
∵△AOC中,AO=CO=AC=2,∴△AOC是边长为2的正三角形,
又∵D为CO的中点,∴AD⊥SC且AD=$\sqrt{3}$.
则${S}_{△SAC}=\frac{1}{2}SC•AD=\frac{1}{2}×4×\sqrt{3}=2\sqrt{3}$.
∵BC=BS=2$\sqrt{2}$,∴BO⊥SC且BO=2.
又AO=2,AB=2$\sqrt{2}$,∴BO2+AO2=AB2,即BO⊥AO,
∵AO∩SC=O,∴BO⊥平面SAC,
因此,VS-ABC=VB-SAC=$\frac{1}{3}×2\sqrt{3}×2=\frac{4\sqrt{3}}{3}$.
故选:D.
点评 本题给出球的直径与两条直线所成角的大小,求球内接三棱锥的体积.着重考查了球的性质、球内接多面体、线面垂直的判定定理与锥体体积求法等知识,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
9.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 63.6 | B. | 65.5 | C. | 72 | D. | 67.7 |
5.已知(x2+2x+3y)5的展开式中x5y2( )
| A. | 60 | B. | 180 | C. | 520 | D. | 540 |
12.已知平面直角坐标系xoy,以O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的参数方程为$\left\{\begin{array}{l}x=2cosφ\\ y=2+2sinφ\end{array}\right.(φ为参数)$.点A,B是曲线C上两点,点A,B的极坐标分别为$({ρ_1},\frac{π}{3}),({ρ_2},\frac{5π}{6})$.则|AB|=( )
| A. | 4 | B. | $\sqrt{7}$ | C. | $4\sqrt{7}$ | D. | 5 |
9.方程$\sqrt{{{({x-3})}^2}+{y^2}}-\sqrt{{{({x+3})}^2}+{y^2}}=4$化简的结果是( )
| A. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$(x≤-2) | D. | $\frac{y^2}{5}-\frac{x^2}{4}=1$(y$≤-\sqrt{5}$) |
10.若a1,a2,a3,…a20这20个数据的平均数为$\bar x$,方差为0.21,则a1,a2,a3,…a20,$\bar x$这21个数据的方差为( )
| A. | 0.19 | B. | 0.20 | C. | 0.21 | D. | 0.22 |
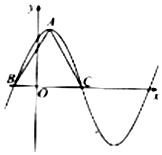 函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.