题目内容
14.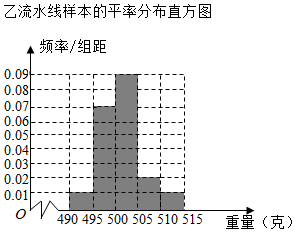 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品,统计结果如表:甲流水线样本的频数分布表
| 产品重量(克) | 频数 |
| [490,495) | 6 |
| [495,500) | 8 |
| [500,505) | 14 |
| [505,510) | 8 |
| [510,515] | 4 |
(2)从乙流水线上重量值落在[505,515]内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
分析 (1)由图1知,甲样本中合格品的频数,进而可得频率;
(2)根据古典概型概率计算公式,可得答案.
解答 解:(1)由表知甲流水线样本中合格品数为8+14+8=30,
故甲流水线样本中合格品的频率为$\frac{30}{40}=0.75$.
(2)乙流水线上重量值落在[505,515]内的合格产品件数为0.02×5×40=4,
不合格产品件数为0.01×5×40=2.
设合格产品的编号为a,b,c,d,不合格产品的编号为e,f.
抽取2件产品的基本事件空间为
Ω={(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)}共15个.
用A表示“2件产品恰好只有一件合格”这一基本事件,则A={(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f)}共8个,
故所求概率$P=\frac{8}{15}$.
点评 本题考查的知识点是古典概型概率公式,难度不大,属于基础题.

练习册系列答案
相关题目
5.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+2≥0}\\{x-y+3≥0}\\{2x+y-3≤0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 6 | B. | $\frac{3}{2}$ | C. | 0 | D. | 12 |
9.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 63.6 | B. | 65.5 | C. | 72 | D. | 67.7 |
4.已知椭圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1的左、右焦点分别为F1,F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1于点P,线段PF2的垂直平分线与l1的交点的轨迹为曲线C2,若点Q是C2上任意的一点,定点A(4,3),B(1,0),则|QA|+|QB|的最小值为( )
| A. | 6 | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
5.已知(x2+2x+3y)5的展开式中x5y2( )
| A. | 60 | B. | 180 | C. | 520 | D. | 540 |
 直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.